
【题目】定义在![]() 上的函数
上的函数![]() 为增函数,对任意
为增函数,对任意![]() 都有
都有![]() (
(![]() 为常数)
为常数)
(1)判断![]() 为何值时,
为何值时,![]() 为奇函数,并证明;
为奇函数,并证明;
(2)设![]() ,
,![]() 是
是![]() 上的增函数,且
上的增函数,且![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)若![]() ,
,![]() ,
,![]() 为
为![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() .
.
【答案】(1)![]()
![]() 是奇函数(2)
是奇函数(2)![]() (3)
(3)![]()
【解析】试题分析: (1)根据定义在R上的奇函数的性质,有![]() ,求得k的值,再根据
,求得k的值,再根据![]() ,赋值
,赋值![]() ,即可得到
,即可得到![]() 与
与![]() 之间的关系,根据奇函数的定义,即可证得结论;
之间的关系,根据奇函数的定义,即可证得结论;
(2)将![]() 代入恒等式可得
代入恒等式可得![]() ,再利用恒等式进行赋值,将3转化为f(2),再根据f(x)的单调性去掉“f”,转化为
,再利用恒等式进行赋值,将3转化为f(2),再根据f(x)的单调性去掉“f”,转化为![]() 对任意
对任意![]() 恒成立,采用换元法,再用变量分离出结果
恒成立,采用换元法,再用变量分离出结果
(3)实际是找数列![]() 的最大值,根据通项
的最大值,根据通项![]() 的正负情况,前四项都是正数,从第五项起是负数,所以很容易找出
的正负情况,前四项都是正数,从第五项起是负数,所以很容易找出![]() 的最大值为
的最大值为![]() ,再根据f(x)的单调性的结果;
,再根据f(x)的单调性的结果;
试题解析:
(1)若![]() 在
在![]() 上为奇函数,则
上为奇函数,则![]() ,令
,令![]()
则![]() ,所以
,所以![]()
证明:由![]() ,令
,令![]() ,
,![]() ,则
,则![]()
又![]() ,则有
,则有![]() ,即
,即![]() 对任意
对任意![]() 成立,
成立,
所以![]() 是奇函数.
是奇函数.
(2)因为![]() ,所以
,所以![]()
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
又![]() 是
是![]() 上的增函数,所以
上的增函数,所以![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立.令
恒成立.令![]() ,则
,则![]() 恒成立,
恒成立,![]() ,令
,令![]() ,g(t)在(0,1+
,g(t)在(0,1+![]() )递减,在
)递减,在![]() 递增,
递增,![]() 最小值为g(
最小值为g(![]() 所以实数
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(3)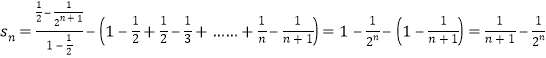
因为![]() ;
;
当n≥5时,
![]() ,而
,而![]() >0得
>0得![]()
所以,当n≥5时,![]() <0,所以对任意n∈N*恒有
<0,所以对任意n∈N*恒有![]() 故k=4, ∵f(x)是增函数,所以
故k=4, ∵f(x)是增函数,所以![]()


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,函数
,函数![]() .
.
(1)求![]() 的定义域
的定义域![]() 及其零点;
及其零点;
(2)讨论并用函数单调性定义证明函数![]() 在定义域
在定义域![]() 上的单调性;
上的单调性;
(3)设![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,在平面直角坐标系
轴的正半轴,建立平面直角坐标系,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() (a﹣ccosB)=bsinC.
(a﹣ccosB)=bsinC.
(1)求角C的大小;
(2)若c=2,则当a,b分别取何值时,△ABC的面积取得最大值,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①函数![]() 的零点有2个;
的零点有2个;
②函数![]() 的最小正周期是
的最小正周期是![]() ;
;
③命题“函数![]() 在
在![]() 处有极值,则
处有极值,则![]() ”的否命题是真命题;
”的否命题是真命题;
④![]() .
.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器使用时间较长,但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,如表为抽样试验结果:
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有 缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(1)用相关系数r对变量y与x进行相关性检验;
(2)如果y与x有线性相关关系,求线性回归方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?(结果保留整数)
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数计算公式: ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com