
【题目】已知等比数列{an}满足:a1= ![]() ,a1 , a2 , a3﹣
,a1 , a2 , a3﹣ ![]() 成等差数列,公比q∈(0,1)
成等差数列,公比q∈(0,1)
(1)求数列{an}的通项公式;
(2)设bn=2nan , 求数列{bn}的前n项和Sn .
【答案】
(1)解:设等比数列{an}公比为q,
∵ ![]() ,
, ![]() 成等差数列,
成等差数列,
∴ ![]() ,即
,即 ![]() ,
,
整理得4q2﹣8q+3=0,
解得 ![]() 或
或 ![]() .
.
又∵q∈(0,1),
∴ ![]() ,
,
∴ ![]()
(2)解:根据题意得bn=2nan= ![]() ,
, ![]() ,①
,①
![]() ,②
,②
②﹣①得: ![]()
= ![]()
= 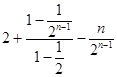
= ![]()
【解析】(1)利用a1 , a2 , a3﹣ ![]() 成等差数列.建立等量关系式,求出通项公式.;(2)写出数列{bn}的通项公式,然后写出前n项和的表达式通过错位相减法求解即可.
成等差数列.建立等量关系式,求出通项公式.;(2)写出数列{bn}的通项公式,然后写出前n项和的表达式通过错位相减法求解即可.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系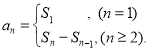 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图. 
(1)若该校高一年级共有学生1000人,试估计成绩不低于60分的人数;
(2)为了帮助学生提高数学成绩,学校决定在随机抽取的50名学生中成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x![]() 时,
时,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法,对于求一个n次多项式函数fn(x)=anxn+an﹣1xn﹣1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和 ![]() 乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
A.﹣5×3=﹣15
B.0.5×3+4=5.5
C.3×33﹣5×3=66
D.0.5×36+4×35=1336.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知☉O1与☉O2相交于A,B两点,过点A作☉O1的切线交☉O2于点C,过点B作两圆的割线,分别交☉O1、☉O2于点D、E,DE与AC相交于点P.若AD是☉O2的切线,且PA=6,PC=2,BD=9,则AB的长为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
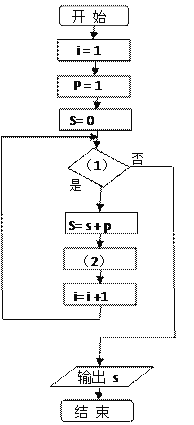
【题目】给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.将右边给出的程序框图补充完整,
(1)___________________ (2)_______________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段AB中点为C,当线段AB的两个端点A和B分别在x轴和y轴上运动时,C点的轨迹为曲线C1;
(1)求曲线C1的方程;
(2)直线 ![]() ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com