
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() .
.
(Ⅰ)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(Ⅱ)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求四棱锥
,求四棱锥![]() 体积的最大值.
体积的最大值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() :
:![]() 上的点按坐标变换
上的点按坐标变换![]() ,得到曲线
,得到曲线![]() ,
,![]() 为
为![]() 与
与![]() 轴负半轴的交点,经过点
轴负半轴的交点,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,与曲线
,与曲线![]() 的交点分别为
的交点分别为![]() ,
,![]() (点
(点![]() 在第二象限).
在第二象限).
(Ⅰ)写出曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
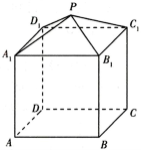
【题目】如图是一个由正四棱锥![]() 和正四棱柱
和正四棱柱![]() 构成的组合体,正四棱锥的侧棱长为6,
构成的组合体,正四棱锥的侧棱长为6,![]() 为正四棱锥高的4倍.当该组合体的体积最大时,点
为正四棱锥高的4倍.当该组合体的体积最大时,点![]() 到正四棱柱
到正四棱柱![]() 外接球表面的最小距离是( )
外接球表面的最小距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: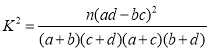 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:cm)落在各个小组的频数分布如下表:
数据分组 | [12.5,15.5) | [15.5,18.5) | [18.5,21.5) | [21.5,24.5) | [24.5,27.5) | [27.5,30.5) | [30.5,33.5) |
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在[27.5,33.5]内的概率;
(2)求这50件产品尺寸的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() (
(![]() ).
).
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]() ;(2)
;(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且对任意n
,且对任意n![]() ,
,![]() 恒成立.
恒成立.
(1)求证:数列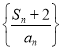 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,已知
,已知![]() ,
,![]() ,
,![]() (2<i<j)成等差数列,求正整数i,j.
(2<i<j)成等差数列,求正整数i,j.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知可导函数f(x)的定义域为![]() ,且满足
,且满足![]() ,
,![]() ,则对任意的
,则对任意的![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com