[题目]已知双曲线C:.则( )A.双曲线C的离心率等于半焦距的长B.双曲线与双曲线C有相同的渐近线C.双曲线C的一条准线被圆x2+y2＝1截得的弦长为D.直线y＝kx+b(k.bR)与双曲线C的公共点个数只可能为0.1.2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知双曲线C：，则( )

A.双曲线C的离心率等于半焦距的长

B.双曲线与双曲线C有相同的渐近线

C.双曲线C的一条准线被圆x2＋y2＝1截得的弦长为

D.直线y＝kx＋b(k，bR)与双曲线C的公共点个数只可能为0，1，2

【答案】ACD

【解析】

根据双曲线的几何性质，直线和双曲线的位置关系，直线和圆的位置关系等知识对选项逐一分析，由此确定正确选项.

双曲线焦点在轴上，且，渐近线为，准线方程为.

对于A选项，双曲线的离心率为，所以A选项正确.

对于B选项，双曲线的渐近线为，与曲线的渐近线不相同，故B选项错误.

对于C选项，双曲线的一条准线方程为代入，解得，所以弦长为，所以C选项正确.

对于D选项，直线与双曲线的公共点个数可能为，故D选项正确.

故选：ACD

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数

（1）若函数在点处切线斜率为0，求的值；

（2）求函数的单调递增区间；

（3）若在处取得极大值，求的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】十九大提出：坚决打赢脱贫攻坚战，做到精准扶贫，我省某帮扶单位为帮助定点扶贫村真正脱贫，坚持扶贫同扶智相结合，帮助贫困村种植脐橙，并利用互联网电商进行销售，为了更好销售，现从该村的脐橙树上随机摘下100个脐橙进行测重，其质量分布在区间（单位：克），统计质量的数据作出其频率分布直方图如图所示：

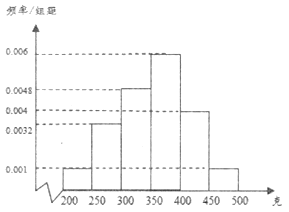
（1）按分层抽样的方法从质量落在，的脐橙中随机抽取5个，再从这5个脐橙中随机抽2个，求这2个脐橙质量至少有一个不小于400克的概率；

（2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的脐橙种植地上大约还有100000个脐橙待出售，某电商提出两种收购方案：

A.所有脐橙均以7元/千克收购；

B.低于350克的脐橙以2元/个收购，其余的以3元/个收购

请你通过计算为该村选择收益较好的方案.

（参考数据：（）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数．

（1）当时，求函数在点处的切线方程；

（2）若函数的图象与轴交于两点，且，求的取值范围；

（3）在（2）的条件下，证明：为函数的导函数）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知正实数，函数 .

（1）讨论函数的单调性；

（2）若在内有解，求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设等差数列的公差d大于0，前n项的和为．已知＝18，，，成等比数列．

（1）求的通项公式；

（2）若对任意的，都有k(＋18)≥恒成立，求实数k的取值范围；

（3）设()．若s，t，s＞t＞1，且，求s，t的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】两地相距，现计划在两地间以为端点的线段上，选择一点处建造畜牧养殖场，其对两地的影响度与所选地点到两地的距离有关，对地和地的总影响度为对地和地的影响度之和，记点到地的距离为，建在处的畜牧养殖场对地和地的总影响度为.统计调查表明：畜牧养殖场对地的影响度与所选地点到地的距离成反比，比例系数为；对地的影响度与所选地点到地的距离成反比，比例系数为，当畜牧养殖场建在线段中点处时，对地和地的总影响度为.