
【题目】某单位![]() 名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组
名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
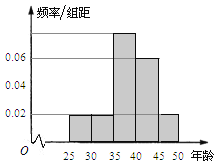
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第![]() 组的员工人数分别是多少?
组的员工人数分别是多少?
(II)为了交流读书心得,现从上述![]() 人中再随机抽取
人中再随机抽取![]() 人发言,设
人发言,设![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有![]() 的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示. 
(1)下表是年龄的频数分布表,求正整数a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,直线AB的方程为3x﹣2y﹣1=0,直线AC的方程为2x+3y﹣18=0.直线BC的方程为3x+4y﹣m=0(m≠25).
(1)求证:△ABC为直角三角形;
(2)当△ABC的BC边上的高为1时,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)求 ![]() 的值;
的值;
(3)已知A(1,cosx)、B(1+cosx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角A,B,C所对的边分别为a,b,c,向量m=(2sin B,- ![]() ),n=
),n=![]() ,且m∥n.
,且m∥n.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 中的
中的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.67.7万元
C.65.5万元
D.72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 到坐标原点的距离和它到直线
到坐标原点的距离和它到直线![]() 的距离之比是一个常数
的距离之比是一个常数![]() .
.
(1)求点![]() 的轨迹;
的轨迹;
(2)若![]() 时得到的曲线是
时得到的曲线是![]() ,将曲线
,将曲线![]() 向左平移一个单位长度后得到曲线
向左平移一个单位长度后得到曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,过
,过![]() 的直线
的直线![]() 分别交曲线
分别交曲线![]() 于点
于点![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com