
【题目】已知A,B,C分别为△ABC的三边a,b,c所对的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且![]() ,求边c的长.
,求边c的长.
【答案】(1)![]() ;(2)6
;(2)6
【解析】
(1)由向量数量积的坐标运算及两角和的正弦公式可得:sin 2C=sin C,再结合二倍角的正弦公式即可得解;
(2)由正弦定理可得2c=a+b,结合题设可得ab=36,再由余弦定理c2=a2+b2-2abcos C运算即可得解.
解:(1)由已知得![]() =sin Acos B+cos Asin B=sin(A+B),
=sin Acos B+cos Asin B=sin(A+B),
因为A+B+C=π,
所以sin(A+B)=sin(π-C)=sin C,
所以![]() =sin C,又
=sin C,又![]() =sin 2C,
=sin 2C,
所以sin 2C=sin C,即![]() ,
,
![]() ,
,![]() ,所以cos C=
,所以cos C=![]() ,所以C=
,所以C=![]() .
.
(2)因为sin A,sin C,sin B成等差数列,
则![]() ,
,
由正弦定理得2c=a+b.
因为![]() ,即
,即![]() ,
,
所以abcos C=18,所以ab=36.
由余弦定理得c2=a2+b2-2abcos C=(a+b)2-3ab,
所以c2=4c2-3×36,
所以c2=36,所以c=6.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
(1)若要求圆柱体罐子的侧面积最大,应如何截取?
(2)若要求圆柱体罐子的体积最大,应如何截取?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() ,直线l:
,直线l:![]() .
.
![]() 若直线l与圆O交于不同的两点A、B,当
若直线l与圆O交于不同的两点A、B,当![]() 为锐角时,求k的取值范围;
为锐角时,求k的取值范围;
![]() 若
若![]() ,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,则直线CD是否过定点?若是,求出定点,并说明理由.
,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,则直线CD是否过定点?若是,求出定点,并说明理由.
![]() 若EF、GH为圆O的两条相互垂直的弦,垂足为
若EF、GH为圆O的两条相互垂直的弦,垂足为![]() ,求四边形EGFH的面积的最大值.
,求四边形EGFH的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】事件一:假设某地区有高中生2400人,初中生10900人,小学生11000人.为了了解该地区学生的视力健康状况,从中抽取![]() 的学生进行调查.事件二:某校为了了解高一年级学生对教师教学的满意率,打算从高一年级500名学生中抽取50名进行调查.对于事件一和事件二,恰当的抽样方法分别是( )
的学生进行调查.事件二:某校为了了解高一年级学生对教师教学的满意率,打算从高一年级500名学生中抽取50名进行调查.对于事件一和事件二,恰当的抽样方法分别是( )
A. 系统抽样,分层抽样
B. 系统抽样,简单随机抽样
C. 简单随机抽样,系统抽样
D. 分层抽样,系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,AB AC,点E,F分别在棱BB1,CC1上(均异于端点),且∠ABE∠ACF,AE⊥BB1,AF⊥CC1.
求证:(1)平面AEF⊥平面BB1C1C;
(2)BC //平面AEF.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且![]() .记
.记![]() (i1,2,3,4).
(i1,2,3,4).
(1)求证:数列![]() 不是等差数列;
不是等差数列;
(2)设![]() ,
, ![]() .若数列
.若数列![]() 是等比数列,求b2关于d的函数关系式及其定义域;
是等比数列,求b2关于d的函数关系式及其定义域;
(3)数列![]() 能否为等比数列?并说明理由.
能否为等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A﹣BCD,则在三棱锥A﹣BCD中,下列判断正确的是_____.(写出所有正确的序号)

①平面ABD⊥平面ABC
②直线BC与平面ABD所成角是45°
③平面ACD⊥平面ABC
④二面角C﹣AB﹣D余弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 上的点,且与顶点不重合.
上的点,且与顶点不重合.
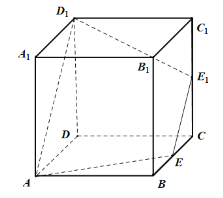
(1)若直线![]() 与
与![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(ⅰ)求证:几何体![]() 为棱台;
为棱台;
(ⅱ)求棱台![]() 的体积.
的体积.
(附:棱台的体积公式![]() ,其中
,其中![]() 、
、![]() 分别为棱台上下底面积,
分别为棱台上下底面积,![]() 为棱台的高)
为棱台的高)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com