
【题目】已知双曲线![]() 的右焦点为
的右焦点为![]() ,
, ![]() 是双曲线C上的点,
是双曲线C上的点, ![]() ,连接
,连接![]() 并延长
并延长![]() 交双曲线C与点P,连接
交双曲线C与点P,连接![]() ,若
,若![]() 是以
是以![]() 为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】如图,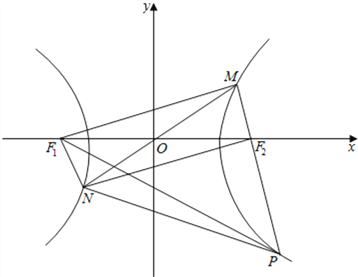
设F1为双曲线左焦点,连接MF1,NF1,则:
由对称性可知四边形F1NF2M
为平行四边形;
又△NF2P是以∠NF2P为顶角的等腰直角三角形,
可得∠MF2N=90°;
∴F1NF2M为矩形;
设|MF2|=x,由双曲线的定义可得,
|MF1|=2a+x;
∴|PF2|=|NF2|=|MF1|=2a+x;
∴|PF1|=2a+|PF2|=4a+x;
在Rt△MF1F2中有:
(2a+x)2+x2=4c2①;
在Rt△MF1P中有:(2a+x)2+(2a+2x)2=(4a+x)2②;
由②解得,x=a,代回①得:9a2+a2=4c2;
∴c2=![]() a2;∴b2=c2﹣a2=
a2;∴b2=c2﹣a2=![]() a2;
a2; ![]()
∴渐近线方程为:y=±![]() x=±
x=±![]() x.
x.
故答案为:B.


科目:高中数学 来源: 题型:
【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(3)若函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() .设
.设![]() ,其中常数
,其中常数![]() 、
、![]() 满足条件
满足条件![]() ,且
,且![]() .试判断在点
.试判断在点![]() 处的切线斜率的正负,并说明理由.
处的切线斜率的正负,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆中心在坐标原点O,焦点在![]() 轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线
轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线![]() 平行OM,且与椭圆交于A、B两个不同的点。
平行OM,且与椭圆交于A、B两个不同的点。
(Ⅰ)求椭圆方程;
(Ⅱ)若![]() AOB为钝角,求直线
AOB为钝角,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围;
的取值范围;
(Ⅲ)求证直线MA、MB与![]() 轴围成的三角形总是等腰三角形。
轴围成的三角形总是等腰三角形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE. 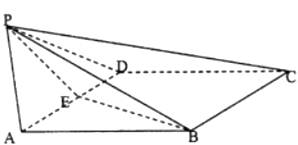
(1)求证:PB⊥BC;
(2)若∠PEB=120°,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com