
已知集合A=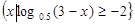 与B=
与B= 满足A∩B=
满足A∩B= ,求实数k的取值范围。
,求实数k的取值范围。
k≤-1或k=0或k≥3.
解析试题分析:易得A={x|-1≤x<3},对B通分可得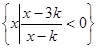 ,有两个实根k,3k,对两根大小分类,分k>0,k=0,k<0加以讨论,当k>0时,B=(k,3k), 欲满足A∩B=
,有两个实根k,3k,对两根大小分类,分k>0,k=0,k<0加以讨论,当k>0时,B=(k,3k), 欲满足A∩B= ,有k≥3;k=0,显然式子是不成立的,则B=
,有k≥3;k=0,显然式子是不成立的,则B= ,显然满足A∩B=
,显然满足A∩B= ;k<0可参考k>0,情形类似,综上,即可得答案.
;k<0可参考k>0,情形类似,综上,即可得答案.
试题解析:集合A等价于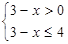 ,得A={x|-1≤x<3},
,得A={x|-1≤x<3},
B= =
=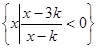 ,当k>0时,B=(k,3k), 欲满足A∩B=
,当k>0时,B=(k,3k), 欲满足A∩B= ,有k≥3;
,有k≥3;
当k=0时,B= ,显然满足A∩B=
,显然满足A∩B= ;当k<0时,B=(3k,k), 欲满足A∩B=
;当k<0时,B=(3k,k), 欲满足A∩B= ,有k≤-1.
,有k≤-1.
综上,k≤-1或k=0或k≥3.
考点:对数不等式,分式不等式,分类讨论.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
设集合A={x|x2<9},B={x|(x-2)(x+4)<0}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为A∪B,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com