D
分析:利用等差数列的定义得到2b=a+c,求出圆心坐标及半径,求出圆心到直线的距离d,利用勾股定理求出弦长,求出最小值.
解答:因为a,b,c成等差数列,
所以2b=a+c.
因为x
2+y
2-2x-2y=0表示以(1,1)为圆心,以

为半径的圆,
则圆心到直线的距离为d=
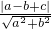
=
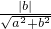
,
则直线ax-by+c=0被曲线x
2+y
2-2x-2y=0截得的弦长,
l=
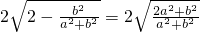
≥2,
当且仅当a=0,且b≠0时,取等号.
所以0截得的弦长的最小值为2,
故选D.
点评:本题考查数列与解析几何的综合运用,是中档题.求直线与圆相交的弦长问题,一般通过构造直角三角形,利用勾股定理求出弦长.


