
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ,
, ![]() ;(2)
;(2)![]()
【解析】
(1)根据条件列方程组解得a,b,根据抛物线焦点坐标所在位置可设抛物线方程形式,再根据焦点坐标求抛物线标准方程,(2)利用斜率设直线![]() 、OB方程,分别与抛物线、椭圆方程联立方程组解得A,B横坐标,再根据A,B横坐标和为0解斜率得A,B坐标,最后根据两点式求直线AB 方程.
、OB方程,分别与抛物线、椭圆方程联立方程组解得A,B横坐标,再根据A,B横坐标和为0解斜率得A,B坐标,最后根据两点式求直线AB 方程.
(1) 由![]() 得
得![]() ,又有
,又有![]() ,代入
,代入![]() ,解得
,解得![]()
所以椭圆方程为![]()
由抛物线的焦点为![]() 得,抛物线焦点在
得,抛物线焦点在![]() 轴,且
轴,且![]() ,
,
抛物线的方程为:![]()
(2)由题意点![]() 位于第一象限,可知直线
位于第一象限,可知直线![]() 的斜率一定存在且大于
的斜率一定存在且大于![]()
设直线![]() 方程为:
方程为:![]() ,
,![]()
联立方程![]() 得:
得:![]() ,可知点
,可知点![]() 的横坐标
的横坐标![]() ,即
,即![]()
因为![]() ,可设直线
,可设直线![]() 方程为:
方程为:![]()
连立方程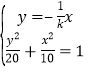 得:
得:![]() ,从而得
,从而得![]()
若线段![]() 的中点在
的中点在![]() 轴上,可知
轴上,可知![]() ,即
,即![]()
有![]() ,且
,且![]() ,解得
,解得![]()
从而得![]() ,
,![]()
直线![]() 的方程:
的方程:![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是________(填序号).
①若![]() ,
,![]() 分别是平面α,β的一个法向量,则
分别是平面α,β的一个法向量,则![]() ∥
∥![]() α∥β;
α∥β;
②若![]() ,
,![]() 分别是平面α,β的一个法向量,则α⊥β
分别是平面α,β的一个法向量,则α⊥β![]() ·
·![]() =0;
=0;
③若![]() 是平面α的一个法向量,
是平面α的一个法向量,![]() 与平面α共面,则
与平面α共面,则![]() ·
·![]() =0;
=0;
④若两个平面的法向量不垂直,则这两个平面一定不垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[0,![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1 , F2为焦点,设图示①②③中的双曲线的离心率分别为e1 , e2 , e3、则e1 , e2 , e3的大小关系为( )
A.e1>e2>e3
B.e1<e2<e3
C.e2=e3<e1
D.e1=e3>e2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足2Sn+an=1;递增的等差数列{bn}满足b1=1,b3=![]() ﹣4.
﹣4.
(1)求数列{an},{bn}的通项公式;
(2)若cn是an , bn的等比中项,求数列{![]() }的前n项和Tn;
}的前n项和Tn;
(3)若c![]() ≤
≤![]() t2+2t﹣2对一切正整数n恒成立,求实数t的取值范围.
t2+2t﹣2对一切正整数n恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(1)求证:BADC=GCAD;
(2)求BM.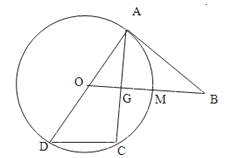
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a、b、c,有下列命题:①若a>b,则ac<bc;②若ac2>bc2,则a>b;③若a<b<0,则a2>ab>b2;④若c>a>b>0,则![]() ;⑤若a>b,
;⑤若a>b,![]() ,则a>0,b<0.其中正确的是________.(填写序号)
,则a>0,b<0.其中正确的是________.(填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.

(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com