
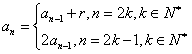 ,其中,r≥0常数。
,其中,r≥0常数。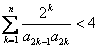 恒成立。
恒成立。  教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆八中高三(上)第四次月考数学试卷(理科)(解析版) 题型:解答题
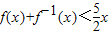 ,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).
,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).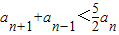 (n∈N*).
(n∈N*).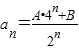 ;
;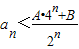 .如果存在,求出A,B的值,如果不存在,说明理由.
.如果存在,求出A,B的值,如果不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2006年北京市海淀区高考数学二模试卷(理科)(解析版) 题型:解答题
 ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,…. ;
;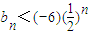 (n∈N*);
(n∈N*); 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有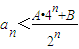 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.查看答案和解析>>
科目:高中数学 来源:2011年湖北省黄冈市高考数学冲刺试卷1(理科)(解析版) 题型:解答题
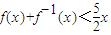 ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….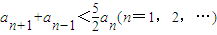 ;
;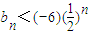 (n∈N*);
(n∈N*);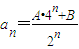 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有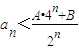 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.查看答案和解析>>
科目:高中数学 来源:2011年湖北省黄冈市高考数学交流试卷(理科)(团风中学)(解析版) 题型:解答题
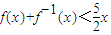 ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….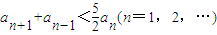 ;
;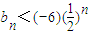 (n∈N*);
(n∈N*);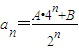 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有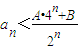 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com