
分析 (1)把曲线C的极坐标方程、直线的参数方程都化为普通方程,再用几何法或判别式法判断直线与圆的位置关系.
(2)联立l与C的方程,求出点A、B的坐标,再计算$\overrightarrow{PA}$•$\overrightarrow{PB}$;或用参数方程直接求$\overrightarrow{PA}•\overrightarrow{PB}$的值;或用几何法求$\overrightarrow{PA}•\overrightarrow{PB}$的值.
解答 解:(1)曲线C的极坐标方程ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),
化为普通方程是x2+y2-2x-2y=0,
即(x-1)2+(y-1)2=2;
所以C是以(1,1)为圆心,半径为$\sqrt{2}$的圆;…(2分)
直线的参数方程$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$(t为参数),
消去参数t得直线的普通方程为y=2x+1;…(4分)
设圆心C(1,1)到直线l的距离为d,
则d=$\frac{|2-1+1|}{{\sqrt{{2^2}+{1^2}}}}=\frac{{2\sqrt{5}}}{5}<\sqrt{2}$,(或用判别式法) …(6分)
所以直线l与曲线C相交.…(7分)
(2)联立l与C的方程得方程组$\left\{\begin{array}{l}y=2x+1\\{x^2}+{y^2}-2x-2y=0\end{array}\right.$,
解得$\left\{\begin{array}{l}x=\frac{{1+\sqrt{6}}}{5}\\ y=\frac{{7+2\sqrt{6}}}{5}\end{array}\right.$或$\left\{\begin{array}{l}x=\frac{{1-\sqrt{6}}}{5}\\ y=\frac{{7-2\sqrt{6}}}{5}\end{array}\right.$,
即A($\frac{{1+\sqrt{6}}}{5}$,$\frac{{7+2\sqrt{6}}}{5}$),B($\frac{{1-\sqrt{6}}}{5}$,$\frac{{7-2\sqrt{6}}}{5}$);…(10分)
所以$\overrightarrow{PA}$=($\frac{{1+\sqrt{6}}}{5}$,$\frac{{2+2\sqrt{6}}}{5}$),$\overrightarrow{PB}$=($\frac{{1-\sqrt{6}}}{5}$,$\frac{{2-2\sqrt{6}}}{5}$);…(12分)
所以$\overrightarrow{PA}•\overrightarrow{PB}$=($\frac{{1+\sqrt{6}}}{5}$,$\frac{{2+2\sqrt{6}}}{5}$)•($\frac{{1-\sqrt{6}}}{5}$,$\frac{{2-2\sqrt{6}}}{5}$)=$-\frac{1}{5}+4(-\frac{1}{5})$=-1.…(14分)
又解:(用参数方程直接求)
将直线参数方程直接代入圆C的普通方程得
t2+(2t+1)2-2t-2(2t+1)=0,
化简得:5t2-2t-1=0,
所以t1t2=$-\frac{1}{5}$…(10分)
所以$\overrightarrow{PA}•\overrightarrow{PB}$=$\sqrt{5}{t_1}•\sqrt{5}{t_2}$=5t1t2=-1(或者用直线参数方程的标准形式)…(14分)
(几何法)过圆心C作AB的垂线交AB于H,则H平分AB,
所以$\overrightarrow{PA}•\overrightarrow{PB}$=$(\overrightarrow{PH}+\overrightarrow{HA})•(\overrightarrow{PH}+\overrightarrow{HB})$
=$(\overrightarrow{PH}+\overrightarrow{HA})•(\overrightarrow{PH}-\overrightarrow{HA})$
=${\overrightarrow{PH}^2}-{\overrightarrow{HA}^2}$
=PH2-HA2
=PH2-(R2-HC2)
=PC2-R2
=-1.
点评 本题考查了直线与圆的应用问题,也考查了参数方程与极坐标的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | -1<x1x2<0 | D. | 1<x1x2<10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{xsinx+cosx}{{x}^{2}}$ | B. | $\frac{xcosx+sinx}{{x}^{2}}$ | C. | $\frac{xcosx-sinx}{{x}^{2}}$ | D. | $\frac{xsinx-cosx}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
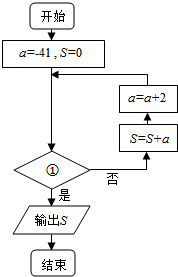
| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com