
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=AD=2,BC=1,![]() .
.
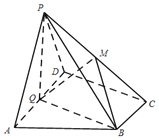
(1)求证:平面PQB⊥平面PAD;
(2)若M是棱PC上的一点,且满足![]() ,求二面角M﹣BQ﹣C的大小.
,求二面角M﹣BQ﹣C的大小.
【答案】(1)证明见解析;
(2)![]()
【解析】
(1)推导出四边形BCDQ是平行四边形,从而![]() ,进而
,进而![]() 平面PQB,由此能证明平面PQB⊥平面PAD.
平面PQB,由此能证明平面PQB⊥平面PAD.
(2)以Q为原点,QA为x轴,QB为y轴,QP为z轴建立空间直角坐标系,求出平面MBQ,BQC的法向量,利用向量法求出二面角M﹣BQ﹣C的大小.
(1)![]() 为AD中点,PA=PD=AD=2,BC=1
为AD中点,PA=PD=AD=2,BC=1
![]()
故四边形BCDQ是平行四边形
![]()
又底面ABCD为直角梯形,AD∥BC,∠ADC=90°
![]() ,又
,又![]()
![]() 平面PQB
平面PQB
![]() 平面PAD
平面PAD
![]() 平面PQB⊥平面PAD.
平面PQB⊥平面PAD.
(2)![]() 平面PQB⊥平面PAD,平面PQB
平面PQB⊥平面PAD,平面PQB![]() 平面PAD=PQ
平面PAD=PQ
![]() PQ⊥平面PAD
PQ⊥平面PAD
以Q为原点,QA为x轴,QB为y轴,QP为z轴建立空间直角坐标系
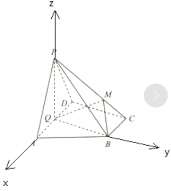
则![]()
设![]() ,即
,即
![]()
![]()
![]()
设平面MAB的法向量为:![]()
则: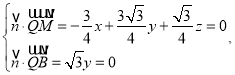 取
取![]()
则![]()
平面BQC的法向量为![]()
设二面角M﹣BQ﹣C的平面角为![]() ,
,
则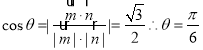
故二面角M﹣BQ﹣C的平面角为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点
上任意一点![]() 向
向![]() 轴作垂线段垂足为
轴作垂线段垂足为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,且满足
上的一点,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,点
两点,点![]() 为轨迹
为轨迹![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点.问:
两点.问:![]() 轴正半轴上是否存在定点使得以
轴正半轴上是否存在定点使得以![]() 为直径的圆过该定点?若存在,求出符合条件的定点坐标;若不存在,请说明理由.
为直径的圆过该定点?若存在,求出符合条件的定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点为(0,1)
(1)求抛物线C的方程;
(2)设直线l2:y=kx+m与抛物线C有唯一公共点P,且与直线l1:y=﹣1相交于点Q,试问,在坐标平面内是否存在点N,使得以PQ为直径的圆恒过点N?若存在,求出点N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() N
N![]() ,
,![]() ≥2,且
≥2,且![]() R.
R.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,令
时,令![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试求函数
时,试求函数![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 在圆
在圆![]() :
:![]() 上.
上.
(1)求实数![]() 的值;
的值;
(2)求过圆心![]() 且与直线
且与直线![]() 平行的直线的方程;
平行的直线的方程;
(3)过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图统计了截止2019年年底中国电动车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
中国电动车充电桩细分产品占比情况:
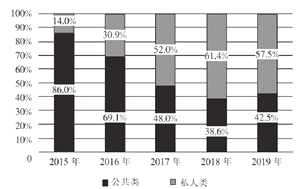
中国电动车充电桩细分产品保有量情况:(单位:万台)
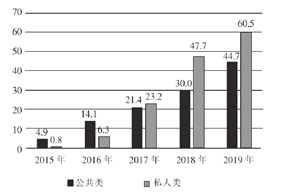
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,直线l交于A,B两点,O为坐标原点,直线OA,OB的斜率分别为k1,k2,若k1k2=﹣2,则△AOB面积的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据国家统计局发布的数据,2019年11月全国CPI(居民消费价格指数),同比上涨4.5%,CPI上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响CPI上涨3.27个百分点.下图是2019年11月CPI一篮子商品权重,根据该图,下列结论错误的是( )
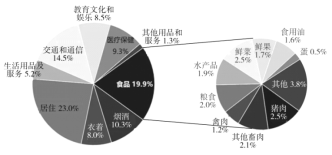
A.CPI一篮子商品中所占权重最大的是居住
B.CPI一篮子商品中吃穿住所占权重超过50%
C.猪肉在CPI一篮子商品中所占权重约为2.5%
D.猪肉与其他畜肉在CPI一篮子商品中所占权重约为0.18%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com