
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45°,求![]() 的值.
的值.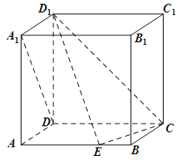
【答案】
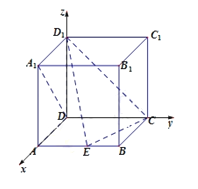
证明:(1)以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,1,2),A1(1,0,1),
设E(1,m,0)(0≤m≤1)![]() =(1,0,1),
=(1,0,1),![]() =(﹣1,﹣m,1),
=(﹣1,﹣m,1),![]()
![]() =﹣1+0+1=0,
=﹣1+0+1=0,
所以DA1⊥ED1.
解:(2)设平面CED1的一个法向量为![]() =(x,y,z),
=(x,y,z),
∵![]() =(0,-1,1),
=(0,-1,1),![]() =(1,m﹣1,0),
=(1,m﹣1,0),
∴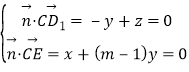 ,取z=1,得y=1,x=1﹣m,得
,取z=1,得y=1,x=1﹣m,得![]() =(1﹣m,1,1).
=(1﹣m,1,1).
∵直线DA1与平面CED1成角为45o,∴sin45°=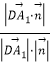 =
=![]() =
=![]() ,
,
解得m=![]() .
.
∴![]() 的值为
的值为![]() .
.
【解析】(1)根据已知条件中的垂直关系,建立空间直角坐标系,要证明DA1⊥ED1,只需证明![]()
![]() =0即可,建立空间直角坐标系后,写出有关点的坐标,得到向量
=0即可,建立空间直角坐标系后,写出有关点的坐标,得到向量![]() 和
和![]() 的坐标,利用向量的数量积的计算公式进行计算.
的坐标,利用向量的数量积的计算公式进行计算.
(2)先利用求平面法向量的计算公式,求出平面CED1的法向量,由已知直线与平面成角为45°,利用夹角公式得到方程,解出![]() 的值.
的值.


科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.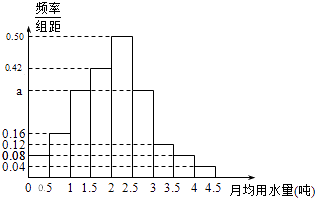
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点;命题q:曲线![]() ﹣
﹣![]() =1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
=1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
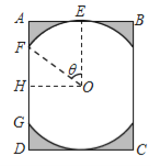
【题目】【苏北三市(连云港、徐州、宿迁)2017届高三年级第三次调研考试】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【扬州市2016—2017学年度第一学期期末检测】(本小题满分14分)
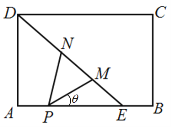
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间,属于酒后驾车;在80mg/100mL(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如表:
酒精含量(mg/100mL) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(1)绘制出检测数据的频率分布直方图(计算并标上选取的y轴单位长度,在图中用实线画出矩形框并用阴影表示),估计检测数据中酒精含量的众数
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的中位数、平均数(请写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
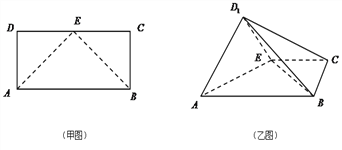
【题目】【2017四川宜宾二诊】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x1 , y1),B(x2 , y2)是函数f(x)= 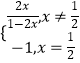 的图象上的任意两点(可以重合),点M在直线x=
的图象上的任意两点(可以重合),点M在直线x= ![]() 上,且
上,且 ![]() =
= ![]() .
.
(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ),求Sn .
),求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com