练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给定椭圆，称圆为椭圆的“伴随圆”.已知点是椭圆上的点

    （1）若过点的直线与椭圆有且只有一个公共点，求被椭圆的伴随圆所截得的弦长：

    （2）是椭圆上的两点，设是直线的斜率，且满足，试问：直线是否过定点，如果过定点，求出定点坐标，如果不过定点，试说明理由。

    【答案】(1) (2)过原点

    【解析】试题分析：（1）分析直线的斜率是否存在，若不存在不符合题意，当存在时设直线，根据直线与圆的关系中弦心距，半径，半弦长构成的直角三角形求解即可；（2）设直线的方程分别为，设点，联立得得同理，计算，同理因为，可得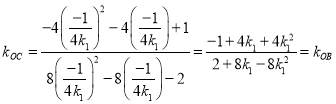，从而可证.

    试题解析：

    （1）因为点是椭圆上的点.

    即椭圆

    伴随圆得同理，计算

    当直线的斜率不存在时：显然不满足与椭圆有且只有一个公共点

    当直接的斜率存在时：设直线与椭圆联立得

    由直线与椭圆有且只有一个公共点得

    解得，由对称性取直线即

    圆心到直线的距离为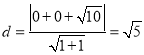

    直线被椭圆的伴随圆所截得的弦长

    （2）设直线的方程分别为

    设点

    联立得

    则得同理

    斜率

    同理因为

    所以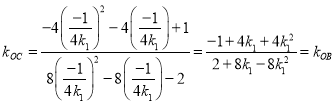 三点共线

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的定义域为{x|x∈R，且x≠0}，对定义域内的任意x1、x2，都有f(x1·x2)＝f(x1)＋f(x2)，且当x>1时，f(x)>0.

    (1)求证：f(x)是偶函数；

    (2)求证：f(x)在(0，＋∞)上是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程为 （其中α为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4sinθ．
    （1）若A，B为曲线C1 ， C2的公共点，求直线AB的斜率；
    （2）若A，B分别为曲线C1 ， C2上的动点，当|AB|取最大值时，求△AOB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥中，垂直于正方形所在的平面，在这个四棱锥的所有表面及面、面中，一定互相垂直的平面有_________对．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等比数列{an}的各项均为正数，且2a3是a2与a6的等比中项，2a1+3a2=16．
    （1）求数列{an}的通项公式；
    （2）设bn=log2a1+log2a2+…+log2an ， 求数列{ }的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an= ，若从{an}中提取一个公比为q的等比数列{ }，其中k1=1，且k1＜k2＜…＜kn ， kn∈N* ， 则满足条件的最小q的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=a（x﹣lnx）+ ﹣ ，a∈R．
    （1）讨论f（x）的单调性；
    （2）当a= 时，证明：f（x）＞f′（x）+ 对于任意的x∈[1，2]成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代儒家要求学生掌握六种基本才艺：礼、乐、射、御、书、数，简称“六艺”，某中学为弘扬“六艺”的传统文化，分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛，现有甲、乙、丙三位选手进入了前三名的最后角逐、规定：每场知识竞赛前三名的得分都分别为（，且）；选手最后得分为各场得分之和，在六场比赛后，已知甲最后得分为26分，乙和丙最后得分都为11分，且乙在其中一场比赛中获得第一名，则下列推理正确的是（ ）

    A. 每场比赛第一名得分为4 B. 甲可能有一场比赛获得第二名

    C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三角形ABC边长为2，将它沿高AD翻折，使点B与点C间的距离为 ，此时四面体ABCD的外接球的表面积为 ．

    查看答案和解析>>

    同步练习册答案