
设函数
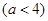
(1)若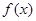 的最小值为3,求
的最小值为3,求 的值;
的值;
(2)求不等式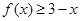 的解集.
的解集.
(1)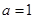 ;(2)
;(2)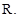
解析试题分析:本题考查绝对值不等式的解法和不等式恒成立问题,考查学生的分类讨论思想和转化能力以及计算能力.第一问,利用不等式的性质,得出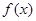 的最小值,列出等式,解出
的最小值,列出等式,解出 的值;第二问,解含参绝对值不等式,用零点分段法去掉绝对值,由于已知中有
的值;第二问,解含参绝对值不等式,用零点分段法去掉绝对值,由于已知中有 和4的大小,所以直接解不等式即可,最后综合上述所得不等式的解集.
和4的大小,所以直接解不等式即可,最后综合上述所得不等式的解集.
试题解析:⑴因为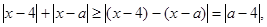
因为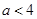 ,所以当且仅当
,所以当且仅当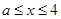 时等号成立,故
时等号成立,故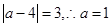 为所求. 4分
为所求. 4分
⑵不等式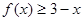 即不等式
即不等式
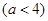 ,
,
①当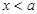 时,原不等式可化为
时,原不等式可化为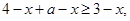
即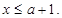
所以,当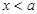 时,原不等式成立.
时,原不等式成立.
②当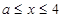 时,原不等式可化为
时,原不等式可化为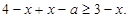
即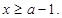 所以,当
所以,当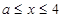 时,原不等式成立.
时,原不等式成立.
③当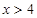 时,原不等式可化为
时,原不等式可化为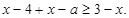
即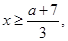 由于
由于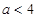 时
时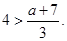
所以,当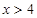 时,原不等式成立.
时,原不等式成立.
综合①②③可知: 不等式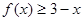 的解集为
的解集为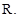 10分
10分
考点:1.不等式的性质;2.绝对值不等式的解法.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
假设若干杯甜度相同的糖水,分别经过下面的试验:
(1)①将所有糖水倒在一起;
②将任意多杯糖水倒在一起.
(2)将某一杯糖水中再加入一小匙糖,糖全都溶化.类经这些实验,分别能得到数学上怎样的关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com