
【题目】某城市要建造一个边长为![]() 的正方形市民休闲公园
的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过对边
图像的一部分,过对边![]() 上一点
上一点![]() 的区域
的区域![]() 内作一次函数
内作一次函数![]() 的图像,与线段
的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
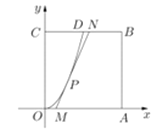
(1)写出函数关系式![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,将四边形
,将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)根据函数y=ax2过点D,求出解析式y=2x2;由![]() 消去y,利用△=0,求出m即可;
消去y,利用△=0,求出m即可;
(2)①写出点P的坐标(t,2t2),代入直线MN的方程,用t表示出直线方程,利用直线方程求出M、N的坐标;
②将四边形MABN的面积S表示成关于t的函数S(t),利用基本不等式即可求出S的最大值.
(1)函数y=ax2过点D(1,2),
代入计算得a=2,
∴y=2x2;
由![]() ,消去y得2x2﹣kx﹣m=0,
,消去y得2x2﹣kx﹣m=0,
由线段MN与曲线OD有且只有一个公共点P,
得△=(﹣k)2+4×2×m=0,
解得m![]() ;
;
(2)设点P的横坐标为t,则0<t<1,
∴点P(t,2t2);
①直线MN的方程为y=kx+b,
即y=kx![]() 过点P,
过点P,
∴kt![]() 2t2,
2t2,
解得k=4t;
y=4tx﹣2t2
令y=0,解得x![]() ,
,
∴M(![]() ,0);
,0);
令y=2,解得x![]() ,
,
∴N(![]() ,2);
,2);
②将四边形MABN的面积S表示成关于t的函数为
S=S(t)=2×2![]() 2×[
2×[![]() (
(![]() )]=4﹣(t
)]=4﹣(t![]() ),其中0<t<1;
),其中0<t<1;
由t![]() 2
2![]() ,当且仅当t
,当且仅当t![]() ,即t
,即t![]() 时“=”成立,
时“=”成立,
所以S≤4![]() ;即S的最大值是4
;即S的最大值是4![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、![]() 后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )

A. 互联网行业从业人员中![]() 后占一半以上
后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 前多
前多
D. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 后多
后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,写出函数
,写出函数![]() 的单调区间(写出必要的过程,不必证明);
的单调区间(写出必要的过程,不必证明);
(3)若存在![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大小相同的2个白球、3个红球;现从中先后有放回地任取球两次,每次取一个球,看完后放回盒中.
(1)求两次取得的球颜色相同的概率;
(2)若在2个白球上都标上数字1,3个红球上都标上数字2,记两次取得的球上数字之和为![]() ,求
,求![]() 的概率分布列与数学期望
的概率分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图像过点
的图像过点![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)若![]() ,试判断函数
,试判断函数![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)设函数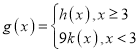 若对每一个不小于
若对每一个不小于![]() 的实数
的实数![]() ,都恰有一个小于
,都恰有一个小于![]() 的实数
的实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com