
【题目】已知实数![]() ,函数
,函数![]() (x∈R).
(x∈R).
(1) 求函数![]() 的单调区间;
的单调区间;
(2) 若函数![]() 有极大值32,求实数a的值.
有极大值32,求实数a的值.
【答案】(1)见解析(2)a=27
【解析】
(1)首先求得函数的导函数,然后分类讨论确定函数的单调区间即可;
(2)由题意得到关于a的方程,解方程求得实数a的值,然后检验是否符合题意即可.
(1)∵f(x)=ax3-4ax2+4ax,
∴f′(x)=3ax2-8ax+4a=a(3x-2)(x-2).
令f′(x)=0,得x=![]() 或x=2.
或x=2.
当a>0时,函数f(x)的单调增区间是![]() ,(2,+∞);单调减区间是
,(2,+∞);单调减区间是![]() .
.
当a<0时,函数f(x)的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ,(2,+∞).
,(2,+∞).
(2)∵f(x)=ax(x-2)2(x∈R)有极大值32,而![]()
∴当x=![]() 时,f(x)取得极大值32,即
时,f(x)取得极大值32,即![]() a
a![]() 2=32,∴a=27.
2=32,∴a=27.
当a=27时,由(1)知,f(x)在![]() 增,在
增,在![]() 递减,符合题设.
递减,符合题设.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
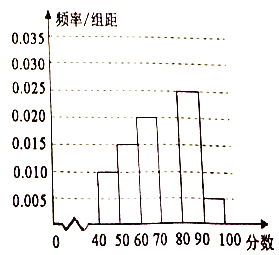
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,其焦点为F,直线过点P(﹣2,0)
(1)若直线l与抛物线C有且仅有一个公共点,求l的方程;
(2)若直线l与抛物线交于不同的两点A、B,求|FA|+|FB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:

(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,过椭圆C的右顶点B任作一条直线
的焦点重合,过椭圆C的右顶点B任作一条直线![]() ,交抛物线
,交抛物线![]() 于A,B两点,且
于A,B两点,且![]() ,
,
(1)试求椭圆C的方程;
(2)过椭圆![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,M,N是椭圆
两点,M,N是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若
两侧的两点.若![]() ,求证:直线MN的斜率
,求证:直线MN的斜率![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() ,直线l:
,直线l:![]() .
.
(1)若直线l与圆O相切,求k的值;
(2)若直线l与圆O交于不同的两点A,B,当![]() 为锐角时,求k的取值范围;
为锐角时,求k的取值范围;
(3)若![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.

![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com