
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 先求出两图象的交点坐标,进而利用定积分即可计算出答案.
解答 解:令x2=cx3(c>0),解得x=0或x=$\frac{1}{c}$,
于是两曲线y=x2与y=cx3(c>0)围成图形的面积=${∫}_{0}^{\frac{1}{c}}({x}^{2}-c{x}^{3})dx$=($\frac{{x}^{3}}{3}-\frac{c{x}^{4}}{4}$)${|}_{0}^{\frac{1}{c}}$=$\frac{1}{12{c}^{3}}$=$\frac{2}{3}$,
∴c=$\frac{1}{2}$
故选B.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{10}$) | B. | (1,$\sqrt{3}$) | C. | (1,3) | D. | (1,10) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
设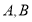 为抛物线
为抛物线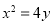 上的两动点,且线段
上的两动点,且线段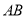 的长为6,
的长为6,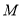 为线段
为线段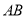 的中点,则点
的中点,则点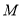 到
到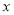 轴的最短距离为 .
轴的最短距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com