
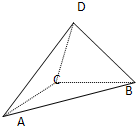
 如图,△ABC与△ACD都是等腰直角三角形,且AD=DC=2,AC=BC,平面DAC⊥平面ABC,如果以ABC平面为水平平面,正视图的观察方向与AB垂直,则三棱锥D-ABC左视图的面积为________.
如图,△ABC与△ACD都是等腰直角三角形,且AD=DC=2,AC=BC,平面DAC⊥平面ABC,如果以ABC平面为水平平面,正视图的观察方向与AB垂直,则三棱锥D-ABC左视图的面积为________.
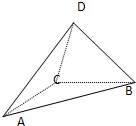
 ,故左视图的高是
,故左视图的高是 ,
,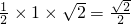 ,
,


科目:高中数学 来源: 题型:
 函数f(x)=2
函数f(x)=2| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲
|
|
| π |
| 3 |
| 1 |
| abc |
| 3 |
查看答案和解析>>
科目:高中数学 来源:扬州大学附属中学高一上学期期末测试卷高一数学[上学期] 题型:044
如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直.若AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.
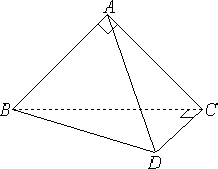
(Ⅰ)求证:三棱锥A-BCD的四个面都是直角三角形;
(Ⅱ)求二面角A-BD-C的正切值.
查看答案和解析>>
科目:高中数学 来源:四川省金堂中学2011-2012学年高二下学期期中考试数学试题 题型:044
如图,△ABC与△DBC均是边长为2的等边三角形,且它们所在平面互相垂直,EA⊥平面ABC,EA=![]() .
.

(1)求证:DE|平面ABC
(2)求二面角A-EC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)设DEF三等分△ABC所在各边,即BC=3BD,CA=3CE,AB=3AF(如图).

求证:△ABC与△DEF有相同的重心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com