练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列各组函数中，表示同一函数的是（ ）
    A.f（x）= ，g（x）=（ ）2
    B.f（x）=（x﹣1）0 ， g（x）=1
    C.f（x） ，g（x）=x+1
    D.f（x）= ，g（t）=|t|

    【答案】D
    【解析】解：f（x）= ，g（x）=（ ）2 ， 函数的定义域不相同，不是相同函数； f（x）=（x﹣1）0 ， g（x）=1，函数的定义域不相同，不是相同函数；
    f（x） ，g（x）=x+1，函数的定义域不相同，不是相同函数；
    f（x）= ，g（t）=|t|，函数的定义域相同，对应法则相同，是相同函数．
    故选：D．
    【考点精析】通过灵活运用判断两个函数是否为同一函数，掌握只有定义域和对应法则二者完全相同的函数才是同一函数即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙两种不同规格的产品，其质量按测试指标分数进行划分，其中分数不小于82分的为合格品，否则为次品.现随机抽取两种产品各100件进行检测，其结果如下：

    测试指标分数

    甲产品

    8

    12

    40

    32

    8

    乙产品

    7

    18

    40

    29

    6

    (1)根据以上数据，完成下面的 列联表，并判断是否有 的有把握认为两种产品的质量有明显差异？

    甲产品

    乙产品

    合计

    合格品

    次品

    合计

    (2)已知生产1件甲产品，若为合格品，则可盈利40元，若为次品，则亏损5元；生产1件乙产品，若为合格品，则可盈利50元，若为次品，则亏损10元.记 为生产1件甲产品和1件乙产品所得的总利润，求随机变量的分布列和数学期望（将产品的合格率作为抽检一件这种产品为合格品的概率）.

    附：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.702

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位共有10名员工，他们某年的收入如下表：

    员工编号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    年薪（万元）

    4

    4.5

    6

    5

    6.5

    7.5

    8

    8.5

    9

    51

    （1）求该单位员工当年年薪的平均值和中位数；

    （2）从该单位中任取2人，此2人中年薪收入高于7万的人数记为，求的分布列和期望；

    （3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元，5.5万元，6万元，8.5万元，预测该员工第五年的年薪为多少？

    附：线性回归方程中系数计算公式分别为：

    ， ，其中为样本均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)讨论函数的单调性；

    (2)当时,记的极大值为,极小值为,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线在点处的切线平行于轴．

    （1）求的单调区间；

    （2）证明：当时， ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）

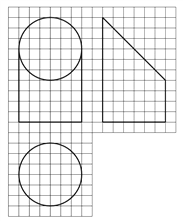
    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知全集U=R，集合A={x|2x+a＞0}，B={x|x2﹣2x﹣3＞0}． （Ⅰ）当a=2时，求集合A∩B；
    （Ⅱ）若A∩（UB）=，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】格纸中每个正方形的边长为1，粗线部分是一个几何体的三视图，则该几何体最长棱的棱长是

    A. 3 B. 6 C. D. 5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    (Ⅰ) 当a＝－1时，求证： ；

    (Ⅱ) 对任意，存在，使成立，求a的取值范围.（其中e是自然对数的底数，e＝2.71828…）

    查看答案和解析>>

    同步练习册答案