
 和所支出的维修费用
和所支出的维修费用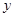 (万元),有如下的统计资料:
(万元),有如下的统计资料:| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
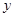 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)科目:高中数学 来源:不详 题型:单选题
 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:零件数 (个) (个) | 10 | 20 | 30 |
加工时间 (分钟) (分钟) | 21 | 30 | 39 |
 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, ,
, .
. ,
, ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 1.08 | 1.12 | 1.19 | 1.28 |
| Y | 2.25 | 2.37 | 2.40 | 2.55 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.若分类变量 和 和 的随机变量 的随机变量 的观测值 的观测值 越大,则“ 越大,则“ 与 与 相关”的可信程度越小 相关”的可信程度越小 |
B.对于自变量 和因变量 和因变量 ,当 ,当 取值一定时, 取值一定时, 的取值具有一定的随机性, 的取值具有一定的随机性, , , 间的这种非确定关系叫做函数关系 间的这种非确定关系叫做函数关系 |
C.相关系数 越接近1,表明两个随机变量线性相关性越弱 越接近1,表明两个随机变量线性相关性越弱 |
D.若分类变量 与 与 的随机变量 的随机变量 的观测值 的观测值 越小,则两个分类变量有关系的把握性越小 越小,则两个分类变量有关系的把握性越小 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | t | 70 |
 =6.5x+17.5,则表中t的值为________.
=6.5x+17.5,则表中t的值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
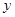 与
与 之间具有很强的线性相关关系,现观测得到
之间具有很强的线性相关关系,现观测得到 的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为
的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为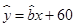 ,其中
,其中 的值没有写上.当
的值没有写上.当 等于
等于 时,预测
时,预测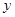 的值为 .
的值为 . |  |  |  |  |
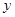 |  |  |  | 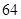 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com