
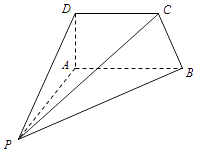
【题目】如图,四棱锥P﹣ABCD中,AD⊥平面PAB,AP⊥AB. 
(1)求证:CD⊥AP;
(2)若CD⊥PD,求证:CD∥平面PAB.
【答案】
(1)证明:因为AD⊥平面PAB,AP平面PAB,所以AD⊥AP.
又因为AP⊥AB,AB∩AD=A,AB平面ABCD,AD平面ABCD,
所以AP⊥平面ABCD.
因为CD平面ABCD,所以CD⊥AP
(2)证明:因为CD⊥AP,CD⊥PD,且PD∩AP=P,PD平面PAD,AP平面PAD,
所以CD⊥平面PAD.①
因为AD⊥平面PAB,AB平面PAB,所以AB⊥AD.
又因为AP⊥AB,AP∩AD=A,AP平面PAD,AD平面PAD,
所以AB⊥平面PAD.②
由①②得CD∥AB,
因为CD平面PAB,AB平面PAB,所以CD∥平面PAB
【解析】(1)推导出AD⊥AP,AP⊥AB,从而AP⊥平面ABCD,由此能证明CD⊥AP.(2)由CD⊥AP,CD⊥PD,得CD⊥平面PAD.再推导出AB⊥AD,AP⊥AB,从而AB⊥平面PAD,进而CD∥AB,由此能证明CD∥平面PAB.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润. 
(1)将T表示为x的函数;
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110))则取x=105,且x=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.y=f(x)的图象关于(π,0)中心对称
B.y=f(x)的图象关于x= ![]() 对称
对称
C.f(x)的最大值为 ![]()
D.f(x)既是奇函数,又是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解开展校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100] |
频数 | 6 | a | 24 | b |

(1)求a,b,c的值;
(2)先用分层抽样的方法从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈,再从这10人中任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(3)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校开展安全教育活动的成效.若
的方差)来评估该校开展安全教育活动的成效.若![]() ≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.
≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是含数1的有限实数集,f(x)是定义在D上的函数。若f(x)的图像绕原点逆时针旋转![]() 后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 0
D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex﹣ax﹣1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2﹣e)x. ①求函数h(x)=f (x)﹣g (x)的单调区间;
②若函数F(x)= ![]() 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1 , x2∈[0,2],使得f(x1)=f(x2),且|x1﹣x2|≥1,求证:e﹣1≤a≤e2﹣e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC= ![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点. 
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() =λ.若CM∥平面AEF,求实数λ的值.
=λ.若CM∥平面AEF,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(Ⅰ)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)预测该路段![]() 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.
参考公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com