练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    甲、乙、丙、丁四位同学计划暑假分别外出旅游，有A、B、C三条线路可选，若每条线路至少有1人选择，则不同的安排方法有（　　）
    分析：从甲、乙、丙、丁四位同学中任取2个同学作为一个整体，共有
    C
    2
    4
    =6种方法，再将这3个同学在A、B、C三条线路上进行全排列，共有
    A
    3
    3
    =6种方法，根据分步计数原理求出不同的安排方法．
    解答：解：先从甲、乙、丙、丁四位同学中任取2个同学作为一个整体，四位同学变为3个，共有
    C
    2
    4
    =6种方法，
    再将这3个同学在A、B、C三条线路上进行全排列，共有
    A
    3
    3
    =6种方法．
    根据分步计数原理，不同的安排方法有6×6=36 种，
    故选 B．
    点评：本题主要考查排列、组合以及分步计数原理的应用，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计选修数学2-1苏教版 苏教版 题型：044

    有甲、乙、丙、丁四位同学独立地做同一道题目：“已知坐标满足方程F(x，y)＝0的点都在曲线C上；那么你能得出怎样的结论？”四人分别有下面的结论：

    甲：曲线C上的点的坐标未必全适合方程F(x，y)＝0；

    乙：凡坐标不适合F(x，y)＝0的点都不在C上；

    丙：不在C上的点的坐标必不适合F(x，y)＝0；

    丁：不在C上的点的坐标有些适合方程，有些不适合方程．

    试判断这四人中谁的说法正确？

    查看答案和解析>>

    科目：高中数学 来源：江苏省2010年高考预测试题数学 题型：解答题

    【必做题】(本题满分10分)

    某单位举办2010年上海世博会知识宣传活动，进行现场抽奖．盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”（世博会吉祥物）图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是‘‘海宝”，即可获奖，否则，均为不获奖．卡片用后后放同盒子，下一位参加者继续重复进行。

    （I）有三人参加抽奖，要使至少一人获奖的概率不低于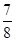，则“海宝”卡至少多少张?

    （2）若有四张“海宝”卡，现有甲乙丙丁四人依次抽奖．用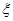表示获奖的人数，求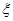的分布列及E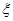的值．

     

    查看答案和解析>>

    同步练习册答案