
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元).每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部销售完.
(万元).每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
【答案】(1)![]() ;(2)年产量为100千件时,该厂在这一商品的生产中所获利润最大为1000万元.
;(2)年产量为100千件时,该厂在这一商品的生产中所获利润最大为1000万元.
【解析】
(1)根据题意可以分成两种情况进行分析讨论:一是当![]() 时,二是当
时,二是当![]() 时,根据年利润=销售收入-成本,这样可以用分段函数形式写出年利润
时,根据年利润=销售收入-成本,这样可以用分段函数形式写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)分别利用配方法和基本不等式求出当![]() 时、当
时、当![]() 时,函数
时,函数![]() 的最大值,通过比较,最后求出函数
的最大值,通过比较,最后求出函数![]() 的最大值.
的最大值.
(1)∵每件商品售价为0.05万元,∴![]() 千件商品销售额为
千件商品销售额为![]() 万元,
万元,
①当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]()
![]() ;
;
②当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]()
![]() .
.
综①②可得,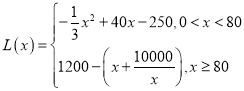 ;
;
(2)①当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元;
万元;
②当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元.
万元.
综合①②,由于![]() ,∴年产量为100千件时,该厂在这一商品的生产中所获利润最大为1000万元.
,∴年产量为100千件时,该厂在这一商品的生产中所获利润最大为1000万元.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=![]() ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。

(1)求证:BC⊥平面ACFE;
(2)若![]() ,求证:AM∥平面BDF.
,求证:AM∥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 左、右焦点分别为
左、右焦点分别为![]() ,
,![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列四个命题:①点
变化时,给出下列四个命题:①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②存在
轴对称;②存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个;③
仅有两个;③![]() 的最小值为2;④
的最小值为2;④![]() 最大值为
最大值为![]() ,其中正确命题的序号是______.
,其中正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究.该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
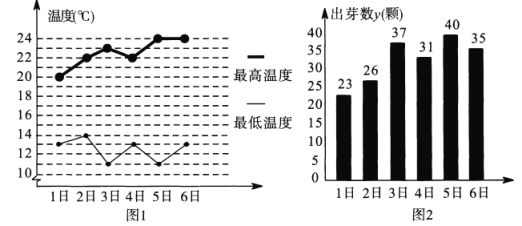
根据上述数据作出散点图,可知绿豆种子出芽数![]() (颗)和温差
(颗)和温差![]() (
(![]() )具有线性相关关系.
)具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() (
(![]() )的回归方程
)的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为11![]() ,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
附: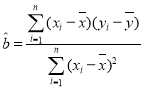
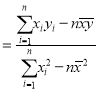 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com