
【题目】(本题满分16分)甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润![]() (元)与年产量
(元)与年产量![]() (吨)满足函数关系
(吨)满足函数关系![]() .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方![]() 元(以下称
元(以下称![]() 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量![]() (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额![]() (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格![]() 是多少?
是多少?
科目:高中数学 来源: 题型:
【题目】设![]() 为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,
为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,![]() ;当两条棱平行时,
;当两条棱平行时,![]() 的值为两条棱之间的距离;当两条棱异面时,
的值为两条棱之间的距离;当两条棱异面时,![]() .
.
(1)求概率![]() ;
;
(2)求![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取![]() 名进行调查,将受访用户按年龄分成
名进行调查,将受访用户按年龄分成![]() 组:
组: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于![]() 岁的概率;
岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,ABCD为矩形,平面PAD⊥平面ABCD. 
(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB= ![]() ,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
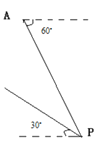
【题目】据监测,在海滨某城市附近的海面有一台风. 台风中心位于城市![]() 的东偏南
的东偏南![]() 方向、距离城市
方向、距离城市![]() 的海面
的海面![]() 处,并以
处,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动(如图示).如果台风侵袭范围为圆形区域,半径
方向移动(如图示).如果台风侵袭范围为圆形区域,半径![]() ,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f0(x)= ![]() (x>0),设fn(x)为fn﹣1(x)的导数,n∈N* .
(x>0),设fn(x)为fn﹣1(x)的导数,n∈N* .
(1)求2f1( ![]() )+
)+ ![]() f2(
f2( ![]() )的值;
)的值;
(2)证明:对任意n∈N* , 等式|nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )|=
)|= ![]() 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高级中学共有学生2000名,各年级男、女生人数如下表:
高一年级 | 高二年级 | 高三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应该在高三年级抽取多少名?
(3)已知![]() ,
,![]() ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90 ![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 ![]() ,五合板2
,五合板2 ![]() ,生产每个书橱需要方木料0.2
,生产每个书橱需要方木料0.2![]() ,五合板1
,五合板1 ![]() ,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com