
 元.公司拟投入
元.公司拟投入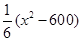 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. 至少应达到10.2万件,每件定价为30元.
至少应达到10.2万件,每件定价为30元. 元时,销售量是(
元时,销售量是(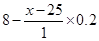 )万件,总收入为
)万件,总收入为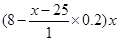 ,不低于原收入,得不等式
,不低于原收入,得不等式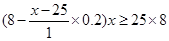 ;(2)关键是弄懂原收入与总投入之和是多少?原收入
;(2)关键是弄懂原收入与总投入之和是多少?原收入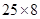 ,总投入
,总投入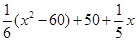 ,明年的销售收入不低于原收入与总投入之和就是不等式
,明年的销售收入不低于原收入与总投入之和就是不等式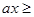
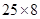
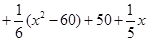 ,根据问题的要求,此式变为
,根据问题的要求,此式变为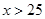 时,
时,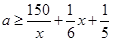 有解(注意不是恒成立),所以
有解(注意不是恒成立),所以 的范围是
的范围是 不小于
不小于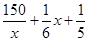 的最小值.
的最小值. 元,依题意,有
元,依题意,有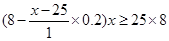 ,
, 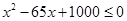 ,解得
,解得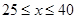 .
.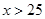 时,
时,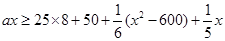 有解,等价于
有解,等价于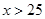 时,
时,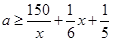 有解,
有解, 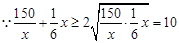 (当且仅当
(当且仅当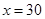 时,等号成立)
时,等号成立)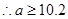 .
. 至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元. 14′
至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元. 14′

科目:高中数学 来源:不详 题型:解答题
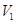 .
.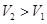 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 吨,此时所需生产费用为(
吨,此时所需生产费用为( )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为 万元,这里
万元,这里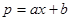 (
( 为常数,
为常数, )
) 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.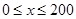 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com