
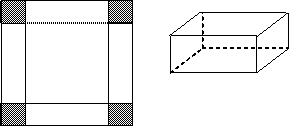
在边长为6的正方形纸板的四角切去相等的正方形,再沿虚线折起,做成一个无盖的方底箱子(如图),
(1)当箱子容积最大时,切去的四个小正方形的边长恰为a,求出a的值;
(2)若将切下来的四个小正方形再按相同方法做成四个无盖的方底箱子,问:当五个箱子的体积总和最大时,第一次切下来的四个小正方形的边长是否仍然为a?说明理由.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
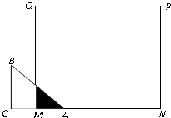 已知如图,等腰三角形ABC的直角边长为a,正方形MNPQ的边为b (a<b),C、M、A、N在同一条直线上,开始时点A与点M重合,让△ABC向右移动,最后点C与点N重合.设三角形与正方形的重合面积为y,点A移动的距离为x,则y关于x的大致图象是( )
已知如图,等腰三角形ABC的直角边长为a,正方形MNPQ的边为b (a<b),C、M、A、N在同一条直线上,开始时点A与点M重合,让△ABC向右移动,最后点C与点N重合.设三角形与正方形的重合面积为y,点A移动的距离为x,则y关于x的大致图象是( )查看答案和解析>>
科目:高中数学 来源: 题型:
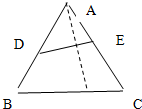 如图,在边长为6的等边三角形纸片△ABC的边AB,AC上分别取点D,E,使沿直线DE折叠三角形纸片后,定点A正好落在边BC上(设为点P),设∠DAP=θ,BD=y.
如图,在边长为6的等边三角形纸片△ABC的边AB,AC上分别取点D,E,使沿直线DE折叠三角形纸片后,定点A正好落在边BC上(设为点P),设∠DAP=θ,BD=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com