
定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。
(1) (2)有,证明见解析(3)
(2)有,证明见解析(3)
【解析】本题以函数为载体,考查新定义,考查恒成立问题,解题的关键是对新定义的理解,恒成立问题采用分离参数法.
(1)写出的函数是下凹的函数即可;
(2)函数 在区间
在区间 上具有性质L,运用定义法加以证明即可。
上具有性质L,运用定义法加以证明即可。
(3)任取x1、x2∈(0,1),且x1≠x2则 >0,只需要
>0,只需要 在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.
在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.
解:(1) (或其它底在(0,1)上的对数函数)。…………2分
(或其它底在(0,1)上的对数函数)。…………2分
(2)函数 在区间
在区间 上具有性质L。…………3分
上具有性质L。…………3分
证明:任取 、
、 ,且
,且
则



 、
、 且
且 ,
,
 ,
,
即 >0,
>0,

所以函数 在区间
在区间 上具有性质L。……………7分
上具有性质L。……………7分
(3)任取 、
、 ,且
,且
则




 、
、 且
且 ,
,
 ,
,
要使上式大于零,必须 在
在 、
、 上恒成立,
上恒成立,
即 ,
,
 ,即实数
,即实数 的取值范围为
的取值范围为 ……………12分
……………12分


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2011年福建省罗源县第一中学高一上学期期中考试数学 题型:解答题
((本题14分)定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数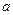 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011年福建省高一上学期期中考试数学 题型:解答题
((本题14分)定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且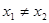 ,都有
,都有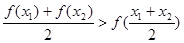 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市八县(市)一中高一(上)期中数学试卷(解析版) 题型:解答题
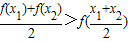 ,则称函数y=f(x)在区间D上具有性质L.
,则称函数y=f(x)在区间D上具有性质L. ,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论. 在区间(0,1)上具有性质L,求实数a的取值范围.
在区间(0,1)上具有性质L,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com