
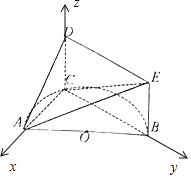
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.

(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由BC⊥AC,BC⊥CD得BC⊥平面ACD,证明四边形DCBE是平行四边形得DE∥BC,故而DE![]() 平面ACD,从而得证面面垂直;
平面ACD,从而得证面面垂直;
(2)建立空间坐标系,求出两半平面的法向量,计算法向量的夹角得出二面角的大小.
(1)证明:∵AB是圆O的直径,∴AC⊥BC,
∵DC⊥平面ABC,BC平面ABC,
∴DC⊥BC,又DC∩AC=C,
∴BC⊥平面ACD,
∵DC∥EB,DC=EB,
∴四边形DCBE是平行四边形,∴DE∥BC,
∴DE⊥平面ACD,
又DE平面ADE,
∴平面ACD⊥平面ADE.
(2)当C点为半圆的中点时,AC=BC=2![]() ,
,
以C为原点,以CA,CB,CD为坐标轴建立空间坐标系如图所示:
则D(0,0,1),E(0,2![]() ,1),A(2
,1),A(2![]() ,0,0),B(0,2
,0,0),B(0,2![]() ,0),
,0),
∴![]() (﹣2
(﹣2![]() ,2
,2![]() ,0),
,0),![]() (0,0,1),
(0,0,1),![]() (0,2
(0,2![]() ,0),
,0),![]() (2
(2![]() ,0,﹣1),
,0,﹣1),
设平面DAE的法向量为![]() (x1,y1,z1),平面ABE的法向量为
(x1,y1,z1),平面ABE的法向量为![]() (x2,y2,z2),
(x2,y2,z2),
则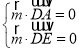 ,
,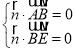 ,即
,即 ,
, ,
,
令x1=1得![]() (1,0,2
(1,0,2![]() ),令x2=1得
),令x2=1得![]() (1,1,0).
(1,1,0).
∴cos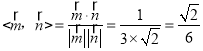 .
.
∵二面角D﹣AE﹣B是钝二面角,
∴二面角D﹣AE﹣B的余弦值为![]() .
.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数![]() (其中
(其中![]() ).
).
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求函数的![]() 反函数
反函数![]()
(3)若两个函数![]() 与
与![]() 在区间
在区间![]() 上恒满足
上恒满足![]() ,则函数
,则函数![]() 与
与![]() 在闭区间
在闭区间![]() 上是分离的.试判断
上是分离的.试判断![]() 的反函数
的反函数![]() 与
与![]() 在闭区间
在闭区间![]() 上是否分离?若分离,求出实数
上是否分离?若分离,求出实数![]() 的取值范围;若不分离,请说明理由.
的取值范围;若不分离,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(1)试估计![]() 岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率;
(2)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: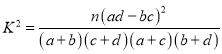 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是我国某城市在2017年1月份至10月份个月最低温与最高温(![]() )的数据一览表.
)的数据一览表.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
|
|
|
|
|
|
|
|
|
已知该城市的各月最低温与最高温具有相关关系,根据这一览表,则下列结论错误的是( )
A.最低温与最高位为正相关
B.每月最高温和最低温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com