
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为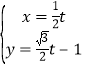 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用代入法消去参数方程中的参数可求直线![]() 的普通方程,极坐标方程展开后,两边同乘以
的普通方程,极坐标方程展开后,两边同乘以![]() ,利用
,利用![]() ,即可得曲线
,即可得曲线![]() 的直角坐标方程;(2)直线
的直角坐标方程;(2)直线![]() 的参数方程代入圆
的参数方程代入圆![]() 的直角坐标方程,利用韦达定理、直线参数方程的几何意义即可得结果.
的直角坐标方程,利用韦达定理、直线参数方程的几何意义即可得结果.
(1)将直线l的参数方程消去参数t并化简,得
直线l的普通方程为![]() .
.
将曲线C的极坐标方程化为![]() .
.
即![]() .∴x2+y2=2y+2x.
.∴x2+y2=2y+2x.
故曲线C的直角坐标方程为![]() .
.
(2)将直线l的参数方程代入![]() 中,得
中,得
![]() .
.
化简,得![]() .
.
∵Δ>0,∴此方程的两根为直线l与曲线C的交点A,B对应的参数t1,t2.
由根与系数的关系,得![]() ,
,![]() ,即t1,t2同正.
,即t1,t2同正.
由直线方程参数的几何意义知,
![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
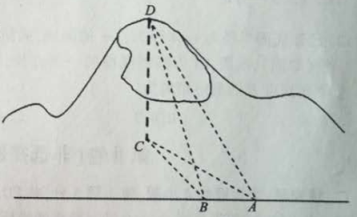
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是水稻产量与施化肥量的一组观测数据(单位:千克/亩):
施化肥量 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
水稻产量 | 320 | 330 | 360 | 410 | 460 | 470 | 480 |
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.一媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取n名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
组数 | 分组(单位:岁) | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 20 | 0.20 |
3 |
| a | 0.35 |
4 |
| 30 | b |
5 |
| 10 | 0.10 |
合计 | n | 1.00 | |
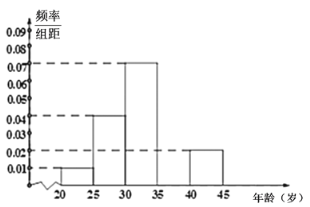
(1)求出表中a,b,n的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查,再从这6名1民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校医务室欲研究昼夜温差大小与高三患感冒人数多少之间的关系,他们统计了2019年9月至2020年1月每月8号的昼夜温差情况与高三因患感冒而就诊的人数,得到如下资料:
日期 | 2019年9月8日 | 2019年10月8日 | 2019年11月8日 | 2019年12月8日 | 2020年1月8日 |
昼夜温差 | 5 | 8 | 12 | 13 | 16 |
就诊人数 | 10 | 16 | 26 | 30 | 35 |
该医务室确定的研究方案是先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.假设选取的是2019年9月8日与2020年1月8日的2组数据.
(1)求就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程
的线性回归方程![]() (结果精确到0.01)
(结果精确到0.01)
(2)若由(1)中所求的线性回归方程得到的估计数据与所选出的检验数据的误差均不超过3人,则认为得到的线性回归方程是理想的,试问该医务室所得线性回归方程是否理想?
参考公式: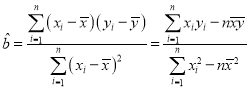 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级的一次月考成绩中随机抽取了 50名学生的成绩(满分100分,且抽取的学生成绩都在![]() 内),按成绩分为
内),按成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图.
五组,得到如图所示的频率分布直方图.
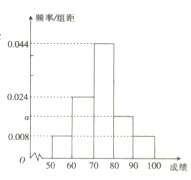
(1)用分层抽样的方法从月考成绩在![]() 内的学生中抽取6人,求分别抽取月考成绩在
内的学生中抽取6人,求分别抽取月考成绩在![]() 和
和![]() 内的学生多少人;
内的学生多少人;
(2)在(1)的前提下,从这6名学生中随机抽取2名学生进行调查,求月考成绩在![]() 内至少有1名学生被抽到的概率.
内至少有1名学生被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com