
如右图(1)所示,定义在区间![]() 上的函数
上的函数![]() ,如果满
,如果满
足:对![]() ,
,![]() 常数A,都有
常数A,都有![]() 成立,则称函数
成立,则称函数
![]() 在区间
在区间![]() 上有下界,其中
上有下界,其中![]() 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数![]() 、
、![]() 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
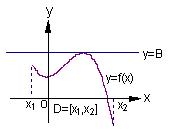 (Ⅰ)试判断函数
(Ⅰ)试判断函数![]() 在
在![]() 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间![]() 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数![]() 在区间
在区间![]() 上
上
有上界的定义,并判断(Ⅰ)中的函数在![]() 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数![]() 在区间
在区间![]() 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数
![]() 在区间
在区间![]() 上有界,函数
上有界,函数![]() 叫做有界函数.试探究函数
叫做有界函数.试探究函数![]() (
(![]()
![]()
![]() 是常数)是否是
是常数)是否是![]() (
(![]()
![]() 、
、![]() 是常数)上的有界函数?
是常数)上的有界函数?
(Ⅰ) A=32 (Ⅱ) 存在常数B=-32(III)![]() 上的有界函数
上的有界函数
:(I)解法1:∵![]() ,由
,由![]() 得
得![]() ,
,
![]() ∵
∵![]() , ∴
, ∴![]() ,---2分
,---2分
∵当![]() 时,
时,![]() ,∴函数
,∴函数![]() 在(0,2)上是减函数;
在(0,2)上是减函数;
当![]() 时,
时,![]() ,∴函数
,∴函数![]() 在(2,+
在(2,+![]() )上是增函数;
)上是增函数;
∴![]() 是函数的在区间(0,+
是函数的在区间(0,+![]() )上的最小值点,
)上的最小值点,![]()
∴对![]() ,都有
,都有![]() ,---4分即在区间(0,+
,---4分即在区间(0,+![]() )上存在常数A=32,使得对
)上存在常数A=32,使得对![]() 都有
都有![]() 成立,∴函数
成立,∴函数![]() 在(0,+
在(0,+![]() )上有下界. ---5分
)上有下界. ---5分
[解法2:![]()
![]()
当且仅当![]() 即
即![]() 时“=”成立∴对
时“=”成立∴对![]() ,都有
,都有![]() ,
,
即在区间(0,+![]() )上存在常数A=32,使得对
)上存在常数A=32,使得对![]() 都有
都有![]() 成立,
成立,
∴函数![]() 在(0,+
在(0,+![]() )上有下界.
)上有下界.
(II)类比函数有下界的定义,函数有上界可以这样定义:
定义在D上的函数![]() ,如果满足:对
,如果满足:对![]() ,
,![]() 常数B,都有
常数B,都有![]() ≤B成立,则称函数
≤B成立,则称函数![]() 在D上有上界,其中B称为函数的上界. -----7分
在D上有上界,其中B称为函数的上界. -----7分
设![]()
![]() 则
则![]() ,由(1)知,对
,由(1)知,对![]() ,都有
,都有![]() ,
,
∴![]() ,∵函数
,∵函数![]() 为奇函数,∴
为奇函数,∴![]()
∴![]() ,∴
,∴![]()
即存在常数B=-32,对![]()
![]() ,都有
,都有![]() ,
,
∴函数![]() 在(-
在(-![]() , 0)上有上界. ---------9分
, 0)上有上界. ---------9分
(III)∵![]() ,由
,由![]() 得
得![]() ,∵
,∵![]()
![]()
∴![]() ∵
∵ ![]() , ∴
, ∴![]() ,----------10分
,----------10分
∵当![]() 时,
时,![]() ,∴函数
,∴函数![]() 在(0,
在(0,![]() )上是减函数;
)上是减函数;
当![]() 时,
时,![]() ,∴函数
,∴函数![]() 在(
在(![]() ,+
,+![]() )上是增函数;
)上是增函数;
∴![]() 是函数的在区间(0,+
是函数的在区间(0,+![]() )上的最小值点,
)上的最小值点, 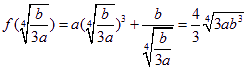 ------11分
------11分
①当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数;
上是增函数;
∴![]()
∵![]() 、
、![]() 是常数,∴
是常数,∴![]() 、
、![]() 都是常数
都是常数
令![]() ,
,
∴对![]() ,
,![]() 常数A,B,都有
常数A,B,都有![]()
即函数![]() 在
在![]() 上既有上界又有下界--------12分
上既有上界又有下界--------12分
②当 ![]() 时函数
时函数![]() 在
在![]() 上是减函数
上是减函数
∴对![]() 都有
都有![]() ∴函数
∴函数![]() 在
在![]() 上有界.-- -13分
上有界.-- -13分
③当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值
上有最小值
![]() =
=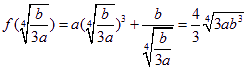
令![]() ,令B=
,令B=![]() 、
、![]() 中的最大者则对
中的最大者则对![]() ,
,![]() 常数A,B,都有
常数A,B,都有![]()
∴函数![]() 在
在![]() 上有界.综上可知函数
上有界.综上可知函数![]() 是
是![]() 上的有界函数---14分
上的有界函数---14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
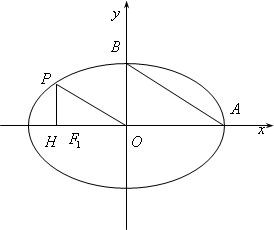 已知在椭圆C:
已知在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定市高三上学期期末调研考试理科数学试卷(解析版) 题型:解答题
某单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中提取10人,然后再从这10人中选4人,那么至少有1人是“运动健将”的概率是多少?
(2)若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com