
【题目】已知点![]() ,过点D作抛物线
,过点D作抛物线![]() 的切线l,切点A在第二象限.
的切线l,切点A在第二象限.
(1)求切点A的纵坐标.
(2)有一离心率为![]() 的椭圆
的椭圆![]() 恰好经过切点A,设切线l与椭圆
恰好经过切点A,设切线l与椭圆![]() 的另一交点为点B,切线l,
的另一交点为点B,切线l,![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() 成等差数列,求椭圆
成等差数列,求椭圆![]() 的方程.
的方程.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,与线段
两点,与线段![]() 和椭圆短轴分别交于两个不同点
和椭圆短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢尔宾斯三角形是一种分形,其具体操作是取一个实心的三角形沿三边中点的连线,将它分成四个小三角形,去掉中间的那一个小三角形,然后对其余三个小三角形重复以上步骤,得到如下的系列图称之为谢尔宾斯:三角形.在第五个图形中,若随机的投入一个质点,则质点落入“空白”处的概率为( )
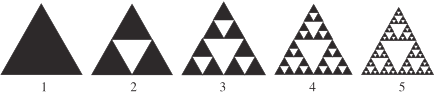
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求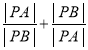 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中记载:“刍(chú)甍(méng)者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”若刍甍的三视图如图所示,主视图是上底为2,下底为4,高为1的等腰梯形,左视图是底边为2的等腰三角形,则该几何体的体积为( ).
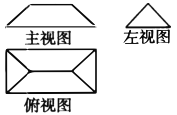
A.![]() B.
B.![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用字母![]() 表示.我们可以通过设计一个试验来估计
表示.我们可以通过设计一个试验来估计![]() 的值:从
的值:从![]() 表示的区域内随机抽取200个实数对
表示的区域内随机抽取200个实数对![]() ,其中x,y两个数能与1构成钝角三角形三边长的数对
,其中x,y两个数能与1构成钝角三角形三边长的数对![]() 共有56个.则用随机模拟的方法估计
共有56个.则用随机模拟的方法估计![]() 的近似值为________.
的近似值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
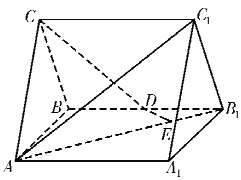
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com