
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(AQI)的检测数据,结果统计如表:
AQI |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于[0,50],(50,100]的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天因空气质量造成的经济损失y(单位:元)与空气质量指数x的关系式为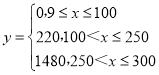 ,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() .9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为X元,求X的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.
【答案】(1)![]() ;(2)(i)详见解析;(ii)会超过;详见解析
;(2)(i)详见解析;(ii)会超过;详见解析
【解析】
(1)利用组合进行计算以及概率表示,可得结果.
(2)(i)写出X所有可能取值,并计算相对应的概率,列出表格可得结果.
(ii)由(i)的条件结合7月与8月空气质量所对应的概率,可得7月与8月经济损失的期望和,最后7月、8月、9月经济损失总额的数学期望与2.88万元比较,可得结果.
(1)设ξ为选取的3天中空气质量为优的天数,
则P(ξ=2)![]() ,P(ξ=3)
,P(ξ=3)![]() ,
,
则这3天中空气质量至少有2天为优的概率
为![]() ;
;
(2)(i)![]() ,
,
![]() ,
,
![]() ,
,
X的分布列如下:
X | 0 | 220 | 1480 |
P |
|
|
|
(ii)由(i)可得:
E(X)=0![]() 220
220![]() 1480
1480![]() 302(元),
302(元),
故该企业9月的经济损失的数学期望为30E(X),
即30E(X)=9060元,
设7月、8月每天因空气质量造成的经济损失为Y元,
可得:![]() ,
,
![]() ,
,![]() ,
,
E(Y)=0![]() 220
220![]() 1480
1480![]() 320(元),
320(元),
所以该企业7月、8月这两个月因空气质量造成
经济损失总额的数学期望为320×(31+31)=19840(元),
由19840+9060=28900>28800,
即7月、8月、9月这三个月因空气质量造成
经济损失总额的数学期望会超过2.88万元.


科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:

根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.243;
作线性相关性检验,求得样本相关系数的绝对值为0.243;
根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.984.
作线性相关性检验,求得样本相关系数的绝对值为0.984.
(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
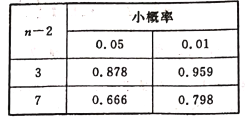
附:相关性检验的临界值表:
(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为![]() ,纸质版本和电子书同时购买的读者比例为
,纸质版本和电子书同时购买的读者比例为![]() ,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准:(单位:吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ……
……![]() 分成9组,制成了如图所示的频率分布直方图
分成9组,制成了如图所示的频率分布直方图
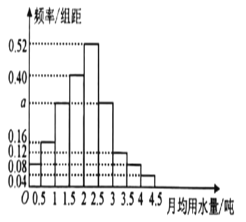
(1)求频率分布直方图中![]() 的值;
的值;
(2)若该市政府看望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由。
的值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,
,![]() ,
,![]() 是其左右顶点,点
是其左右顶点,点![]() 是椭圆
是椭圆![]() 上任一点,且
上任一点,且![]() 的周长为6,若
的周长为6,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆![]() 于
于![]() ,
,![]() 两个不同点,证明:直线
两个不同点,证明:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() ,圆
,圆![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 的交点为A,B,求
的交点为A,B,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,
中,底面四边形ABCD是菱形, ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() .
.
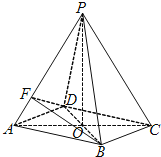
![]() Ⅰ
Ⅰ![]() 求证:
求证: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直线CP与平面BDF所成角的大小;
求直线CP与平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在线段PB上是否存在一点M,使得
在线段PB上是否存在一点M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为椭圆的四个顶点(如图),直线
为椭圆的四个顶点(如图),直线![]() 过右顶点
过右顶点![]() 且垂直于
且垂直于![]() 轴.
轴.
(1)求该椭圆的标准方程;
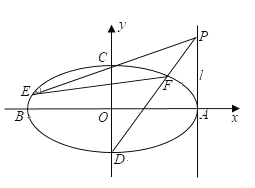
(2)![]() 为
为![]() 上一点(
上一点(![]() 轴上方),直线
轴上方),直线![]() ,
,![]() 分别交椭圆于
分别交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com