练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《九章算术》是我国古代的数学名著，书中有如下间题：“今有甲、乙、丙、丁、戊五人分五饯，令上二人所得与下三人等，且五人所得钱按顺序等次差，问各得几何？”其意思为“甲、乙、丙、丁、戊五人分五钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列，问五人各得多少钱(钱：古代一种重量单位)？”这个问题中丙所得为（ ）

    A. 钱 B. 钱 C. 1钱 D. 钱

    【答案】C

    【解析】设甲、乙、丙、丁、戊分别为：a﹣2d，a﹣d，a，a+d，a+2d，

    由题意可得：a﹣2d+a﹣d+a+a+d+a+2d=5，a﹣2d+a﹣d=a+a+d+a+2d，

    联立解得a=1，d=﹣．

    ∴这个问题中，丙所得为1．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面ABCD为平行四边形，PA⊥底面ABCD，，，，．

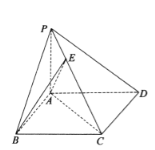
    (1)求证：平面PCA⊥平面PCD；

    (2)设E为侧棱PC上的一点，若直线BE与底面ABCD所成的角为45°，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月14日至15日，“一带一路”国际合作高峰论坛在中国首都北京举行,会议期间,达成了多项国际合作协议.假设甲、乙两种品牌的同类产品出口某国家的市场销售量相等，该国质量检验部门为了解他们的使用寿命，现从这两种品牌的产品中分别随机抽取300个进行测试，结果统计如下图所示,已知乙品牌产品使用寿命小于200小时的概率估计值为.

    (1)求的值;

    (2)估计甲品牌产品寿命小于200小时的概率；

    (3)这两种品牌产品中，某个产品已使用了200小时，试估计该产品是乙品牌的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (是自然对数的底数)

    （1）求证:

    （2）若不等式在上恒成立,求正数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究变量，得到一组样本数据，进行回归分析，有以下结论

    ①残差平方和越小的模型，拟合的效果越好；

    ②用相关指数来刻画回归效果，越小说明拟合效果越好；

    ③在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位

    ④若变量和之间的相关系数为，则变量和之间的负相关很强，以上正确说法的个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为’（为参数）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求和的直角坐标方程；

    （2）已知直线与轴交于点，且与曲线交于，两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）当时，求证：在上为增函数；

    （Ⅲ）若在区间上有且只有一个极值点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正四棱锥中，为底面正方形的中心，侧棱与底面所成的角的正切值为．

    （1）求侧面与底面所成的二面角的大小；

    （2）若是的中点，求异面直线与所成角的正切值；

    （3）问在棱上是否存在一点，使⊥侧面，若存在，试确定点的位置；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来全国各一、二线城市打击投机购房，陆续出台了住房限购令.某市为了进一步了解已购房民众对市政府出台楼市限购令的认同情况，随机抽取了一小区住户进行调查,各户人均月收入(单位：千元)的频数分布及赞成楼市限购令的户数如下表：

    人均月收入

    频数

    6

    10

    13

    11

    8

    2

    赞成户数

    5

    9

    12

    9

    4

    1

    若将小区人均月收入不低于7.5千元的住户称为“高收入户”,人均月收入低于7.5千元的住户称为“非高收入户”

    非高收入户

    高收入户

    总计

    赞成

    不赞成

    总计

    （Ⅰ）求“非高收入户”在本次抽样调杳中的所占比例；

    （Ⅱ）现从月收入在的住户中随机抽取两户，求所抽取的两户都赞成楼市限购令的概率；

    （Ⅲ）根据已知条件完成如图所给的列联表，并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成楼市限购令”有关.

    附：临界值表

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式： ， .

    查看答案和解析>>

    同步练习册答案