
【题目】在边长为2的菱形![]() 中,
中,![]() ,将菱形
,将菱形![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,则所得三棱锥
,则所得三棱锥![]() 的外接球表面积为( )
的外接球表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种产品的质量,从中分别随机抽取了10件样品,测量产品中某种元素的含量(单位:毫克),如图所示是测量数据的茎叶图.规定:当产品中的此中元素的含量不小于18毫克时,该产品为优等品.
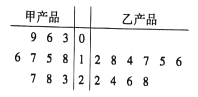
(1)试用样品数据估计甲、乙两种产品的优等品率;
(2)从乙产品抽取的10件样品中随机抽取3件,求抽到的3件样品中优等品数![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从甲产品抽取的10件样品中有放回地随机抽取3件,也从乙产品抽取的10件样品中有放回地随机抽取3件;抽到的优等品中,记“甲产品恰比乙产品多2件”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
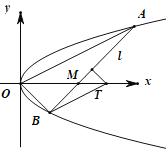
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() ,
,![]() ,
,![]() 两点.当
两点.当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 的面积为
的面积为![]() .
.
0
(1)求抛物线的方程:
(2)设线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() .
.
①证明:![]() 为定值:
为定值:
②若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
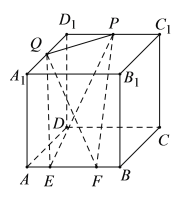
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() (
(![]() 为参数),直线
为参数),直线![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于在
交于在![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求![]() 的参数方程与
的参数方程与![]() 的直角坐标方程;
的直角坐标方程;
(II)射线![]() 与
与![]() 交于异于极点的点
交于异于极点的点![]() ,与
,与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.
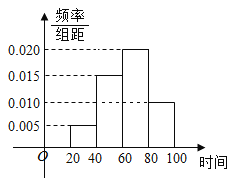
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com