【题目】在△ABC中，∠A=60°，c= 
a．（13分）
（1）求sinC的值；
（2）若a=7，求△ABC的面积．
【答案】
（1）
解：∠A=60°，c= 
a，
由正弦定理可得sinC= sinA= × 
= 
，
（2）
解：a=7，则c=3，
∴C＜A，
由（1）可得cosC= 
，
∴sinB=sin（A+C）=sinAcosC+cosAsinC= × + 
× = 
，
∴S△ABC= acsinB= ×7×3× =6 
．
【解析】（1.）根据正弦定理即可求出答案，
（2.）根据同角的三角函数的关系求出cosC，再根据两角和正弦公式求出sinB，根据面积公式计算即可．
【考点精析】根据题目的已知条件，利用两角和与差的正弦公式和正弦定理的定义的相关知识可以得到问题的答案，需要掌握两角和与差的正弦公式：
；正弦定理:
．
科目：高中数学 来源： 题型：
【题目】对于给定的正整数k，若数列{an}满足：an﹣k+an﹣k+1+…+an﹣1+an+1+…an+k﹣1+an+k=2kan对任意正整数n（n＞k）总成立，则称数列{an}是“P（k）数列”．
（Ⅰ）证明：等差数列{an}是“P（3）数列”；
（Ⅱ）若数列{an}既是“P（2）数列”，又是“P（3）数列”，证明：{an}是等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在同一个平面内，向量 
， 
， 
的模分别为1，1， 
， 与 的夹角为α，且tanα=7， 与 的夹角为45°．若 =m +n （m，n∈R），则m+n= ．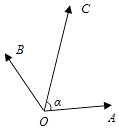 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin2x﹣cos2x﹣2 
sinx cosx（x∈R）．
（Ⅰ）求f（ 
）的值．
（Ⅱ）求f（x）的最小正周期及单调递增区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某园林基地培育了一种新观赏植物，经过了一年的生长发育，技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为
)进行统计，按
分组做出频率分布直方图，并作出样本高度的茎叶图(图中仅列出了高度在
的数据).
（1）求样本容量和频率分布直方图中的
（2）在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取3株,设随机变量
表示所抽取的3株高度在 
内的株数,求随机变量的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，多面体
中， 
两两垂直，且
， 
， 
，
.
(Ⅰ) 若点
在线段
上，且
，求证: 
平面
；
(Ⅱ)求直线
与平面
所成的角的正弦值；
(Ⅲ)求锐二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正△ABC内接于半径为2的圆O，点P是圆O上的一个动点，则 
的取值范围是（ ）
A.[0，6]
B.[﹣2，6]
C.[0，2]
D.[﹣2，2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
