
����Ŀ������Ϊ��̽������![]() �IJ������ʣ����б����£�
�IJ������ʣ����б����£�
| �� | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | �� |
| �� | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.004 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | �� |
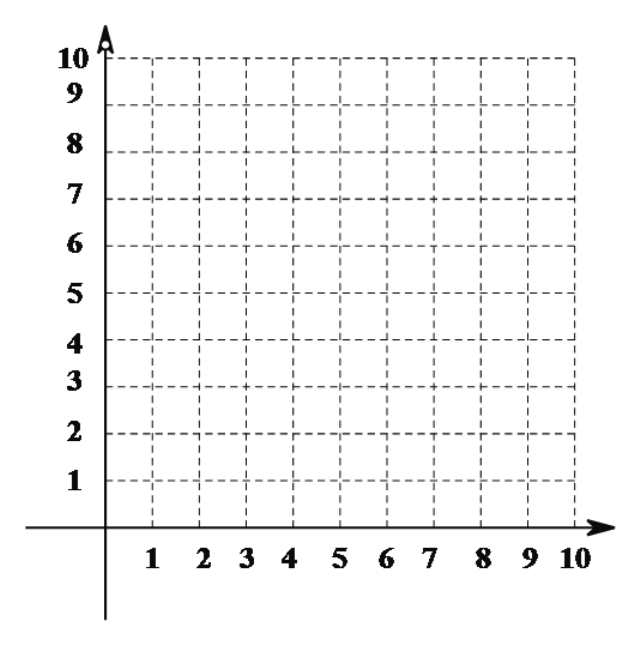
�۲����![]() ֵ��
ֵ��![]() ֵ�仯���ص㣬������µ�����.
ֵ�仯���ص㣬������µ�����.
���ȱȽ������ó������˺���������![]() ���ǵݼ��ģ�
���ǵݼ��ģ�
��1������![]() ������ �ϵ���
������ �ϵ���
��![]() ʱ��
ʱ��![]() = .
= .
��2����������������������˺����Ĵ��ͼ��
��3�����ú��������ԵĶ���֤��������![]() ������
������![]() ��������.
��������.
���𰸡���1��![]() ,2, 4;��2������������3��������
,2, 4;��2������������3��������
��������
��1���ɱ�������ݿ�֪����![]() �ϵݼ�������
�ϵݼ�������![]() �ϵ�����.��
�ϵ�����.��![]() ʱ������Сֵ4
ʱ������Сֵ4
��2�����ݱ���������ϵ�б�����λ�ã���ƽ��������������
��3�����ݵ����ԵĶ���֤������ȡ![]() ����
����![]() ��
��
��![]() ,��
,��![]() ����
����![]() ,��
,��![]() ��
��![]()
�ó�![]()
��1������![]() ������
������![]() �ϵ���.��
�ϵ���.��![]() 2 ʱ��
2 ʱ��![]() = 4
= 4
��2��

��3��֤������ȡ![]() ����
����![]()

��![]() ,��
,��![]() ����
����![]() ,��
,��![]() ��
��![]()
��![]() ������
������![]()
���Ժ���![]() �����䣨0��2�����ǵ����ݼ���.
�����䣨0��2�����ǵ����ݼ���.


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ![]() �У���֪��Բ
�У���֪��Բ![]() ��������Ϊ
��������Ϊ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ���Ե�
���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() Ϊ�뾶��Բ���Ե�
Ϊ�뾶��Բ���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() Ϊ�뾶��Բ�ཻ���ҽ�������Բ
Ϊ�뾶��Բ�ཻ���ҽ�������Բ![]() �ϣ�
�ϣ�
��![]() ������Բ
������Բ![]() �ķ��̣�
�ķ��̣�
��![]() ������Բ
������Բ![]() ��
�� ![]() Ϊ��Բ
Ϊ��Բ![]() ������һ�㣬����
������һ�㣬����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() ��
��
����![]() ��ֵ��
��ֵ��
�ڣ�������������![]() ��������ֵ��
��������ֵ��
�ۣ��Ŀ���������![]() ʱ��
ʱ�� ![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
��2��������![]() ��
��![]() ���м�Сֵ����ʵ��
���м�Сֵ����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x��2|��|2x+l|��
��I����ʽf��x����x�Ľ⼯��
��II ��������ʽf��x����t2��t��x��[��2����1]ʱ���������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У���BAC=90�㣬AB=AC=2��AA1=6����E��F�ֱ�����BB1��CC1�ϣ���BE= ![]() BB1 �� C1F=
BB1 �� C1F= ![]() CC1 ��
CC1 �� 
��1����ƽ��AEF��ƽ��ABC���ɽǦ�������ֵ��
��2����GΪBC���е㣬A1G��ƽ��AEF����H������ ![]() =
= ![]() ����˵�ֵ��
����˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������װ�д�����״��Сһ��������������ͬ��С���������ȡ50����Ϊ�������Ƴ����ǵ�����![]() ��λ����
��λ����![]() ��������������Ϊ
��������������Ϊ![]() ,
,![]() ,
,![]() ,
,![]() ���ɴ˵õ�����������Ƶ�ʷֲ�ֱ��ͼ
���ɴ˵õ�����������Ƶ�ʷֲ�ֱ��ͼ![]() ��ͼ
��ͼ![]() ��
��
��1����![]() ��ֵ���������������ݣ��Թ��ƺ�����С��������������ƽ��ֵ��
��ֵ���������������ݣ��Թ��ƺ�����С��������������ƽ��ֵ��
��2���Ӻ����������ȡ3��С����������![]() �ڵ�С�����Ϊ
�ڵ�С�����Ϊ![]() ����
����![]() �ķֲ��к���ѧ����������ֱ��ͼ�е�Ƶ����Ϊ���ʣ�
�ķֲ��к���ѧ����������ֱ��ͼ�е�Ƶ����Ϊ���ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������
������![]() �ϵ����ݼ�����ʵ��
�ϵ����ݼ�����ʵ��![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�C
����������![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
�ຯ��![]() �ĵ���������Ϊ
�ĵ���������Ϊ![]() ��
��
�ֺ���![]() ������
������![]() �ϵ����ݼ���
�ϵ����ݼ���
��![]()
![]() ��
��
��![]() �����
�����![]() ��
��
��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��ѡC��
��ѡC��
�㾦����֪�����������ϵĵ�����������ķ���
��1�����õ�����⣬ת��Ϊ�������ڸ������ϴ��ڵ����㣨��С�ڵ����㣩�������������⣬һ��ͨ�����������Ϊ��������ֵ��������
��2���������֪�����ĵ������䣬Ȼ������ת��Ϊ�����������Ǻ�����Ӧ�ĵ���������Ӽ����������
�����͡���ѡ��
��������
7
����Ŀ����![]() ������
������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���Ⱥ���ԭͼ���غϣ���
����λ���Ⱥ���ԭͼ���غϣ���![]() ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��С������12��)
��֪����![]() ,
,![]() ��
��![]() .
.
��������![]() �Ķ�����
�Ķ�����
�������ж�![]() ����ż�Բ�����֤����
����ż�Բ�����֤����
��������![]() ʱ����ʹ
ʱ����ʹ![]() ��
��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������ȷ�����Ϊ_______��
��������![]() ��
��![]() �ϵ����ݼ�����ʵ��
�ϵ����ݼ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
�ں���![]() ��ż�������������溯����
��ż�������������溯����
����֪����![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ������
������![]() �Ķ�������
�Ķ�������![]() ��
��
��������![]() ��
��![]() ������Сֵ��4����
������Сֵ��4����![]() ��
��![]() Ϊ���㳣����������
Ϊ���㳣����������![]() ��
��![]() �������ֵ6��
�������ֵ6��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com