
分析 (1)由已知点的坐标求出两个向量的坐标,结合数量积为-1求得sinαcosα的值,把$\frac{{2{{sin}^2}α+sin2α}}{1+tanα}$化切为弦得答案;
(2)化余弦为正弦,利用配方法分类求f(α)=-2cos2α-tsinα-t2+2得最小值,进一步求得t值得答案.
解答 解:(1)$\overrightarrow{AC}=(cosα-3,sinα),\overrightarrow{BC}=(cosα,sinα-3)$,
∵$\overrightarrow{AC}•\overrightarrow{BC}=-1$,
∴cosα(cosα-3)+sinα(sinα-3)=-1,即1-3(cosα+sinα)=-1,得$cosα+sinα=\frac{2}{3}$.
平方得:∴$1+2sinαcosα=\frac{4}{9}$,则$2sinαcosα=-\frac{5}{9}$,
∴$\frac{2si{n}^{2}α+2sinαcosα}{1+tanα}$=$\frac{2sinα(sinα+cosα)}{\frac{sinα+cosα}{cosα}}$=2sinαcosα=$-\frac{5}{9}$;
(2)f(x)=-2cos2α+tsinα-t2+2=$2{(sinα-\frac{t}{4})^2}-\frac{9}{8}{t^2}$,
设sinα=m,∵$α∈(\frac{π}{2},\frac{3π}{2})$,∴m∈(-1,1),
∴$f(m)=2{(m-\frac{t}{4})^2}-\frac{9}{8}{t^2}$.
①当$\frac{t}{4}≤-1$,即t≤-4时,无最小值;
②当$\frac{t}{4}≥1$,即t≥4时,无最小值;
③当$-1<\frac{t}{4}<1$,即-4<t<4时,$sinα=\frac{t}{4}$时取最小值,最小值为$-\frac{9}{8}{t^2}$,
∴$-\frac{9}{8}{t^2}=-1$,$t=±\frac{{2\sqrt{2}}}{3}$,此时$\frac{t}{4}=±\frac{{\sqrt{2}}}{6}∈(-1,1)$,
综上所述,$t=±\frac{{2\sqrt{3}}}{3}$.
点评 本题考查三角函数最值的求法,考查平面向量的坐标运算,训练了利用换元法及配方法求函数的最值,是中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | (2,3) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p,q均为真命题 | |
| B. | “a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 | |
| C. | 在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 | |
| D. | 命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
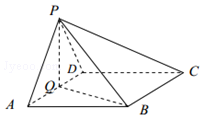 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com