
【题目】已知数列{an}中,a1=1,前n项和Sn= ![]() an .
an .
(1)求a2 , a3 , 及{an}的通项公式.
(2)求{ ![]() }的前n项和Tn , 并证明:1≤Tn<2.
}的前n项和Tn , 并证明:1≤Tn<2.
【答案】
(1)解:由S2= ![]() a2,a1=1,得到3(a1+a2)=4a2,
a2,a1=1,得到3(a1+a2)=4a2,
解得:a2=3a1=3;
由S3= ![]() a3得3(a1+a2+a3)=5a3,
a3得3(a1+a2+a3)=5a3,
解得:a3= ![]() (a1+a2)=6.
(a1+a2)=6.
由题设知a1=1,
当n>1时有an=Sn﹣Sn﹣1= ![]() an﹣
an﹣ ![]() an﹣1,
an﹣1,
整理得:an= ![]() an﹣1.
an﹣1.
于是a1=1,a2= ![]() a1,a3=
a1,a3= ![]() a2,…,an﹣1=
a2,…,an﹣1= ![]() an﹣2,an=
an﹣2,an= ![]() an﹣1,
an﹣1,
将以上n个等式两端分别相乘,整理得an= ![]() ,
,
综上,{an}的通项公式an= ![]()
(2)解:∵ ![]() =
= ![]() ,
,
∴Tn=2[ ![]() +
+ ![]() +…+
+…+ ![]() ]=2(1﹣
]=2(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )=2(1﹣
)=2(1﹣ ![]() )=2﹣
)=2﹣ ![]() <2,即Tn<2,
<2,即Tn<2,
又Tn+1>Tn,{Tn}单调增,
∴Tn>=T1=1,
则1≤Tn<2
【解析】(1)根据已知等式确定出a2 , a3 , 得出{an}的通项公式即可;(2)表示出{ ![]() }的前n项和Tn , 根据前n项和Tn为递增数列,确定出Tn的范围,即可得证.
}的前n项和Tn , 根据前n项和Tn为递增数列,确定出Tn的范围,即可得证.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系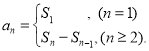 才能正确解答此题.
才能正确解答此题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(2m+1)x+2m(m∈R).
(1)当m=1时,解关于x的不等式xf(x)≤0;
(2)解关于x的不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
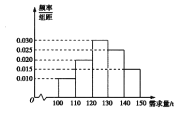
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位: ![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于57000元的概率;
不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
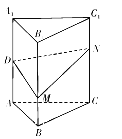
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似地服从正态分布N(70,100).已知成绩在90分以上的学生有12人.
(1)试问此次参赛学生的总数约为多少人?
(2)若成绩在80分以上(含80分)为优,试问此次竞赛成绩为优的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切. 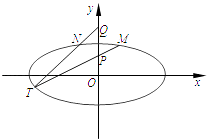
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2).设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T,求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com