
【题目】如图,在平面直角坐标系xOy中,已知圆C:x2+y2﹣4x=0及点A(﹣1,0),B(1,2) 
(1)若直线l平行于AB,与圆C相交于M,N两点,MN=AB,求直线l的方程;
(2)在圆C上是否存在点P,使得PA2+PB2=12?若存在,求点P的个数;若不存在,说明理由.
【答案】
(1)解:圆C的标准方程为(x﹣2)2+y2=4,所以圆心C(2,0),半径为2.
因为l∥AB,A(﹣1,0),B(1,2),所以直线l的斜率为 ![]() ,
,
设直线l的方程为x﹣y+m=0,
则圆心C到直线l的距离为 ![]() .
.
因为 ![]() ,
,
而 ![]() ,所以
,所以 ![]() ,
,
解得m=0或m=﹣4,
故直线l的方程为x﹣y=0或x﹣y﹣4=0.
(2)解:假设圆C上存在点P,设P(x,y),则(x﹣2)2+y2=4,
PA2+PB2=(x+1)2+(y﹣0)2+(x﹣1)2+(y﹣2)2=12,
即x2+y2﹣2y﹣3=0,即x2+(y﹣1)2=4,
因为 ![]() ,
,
所以圆(x﹣2)2+y2=4与圆x2+(y﹣1)2=4相交,
所以点P的个数为2
【解析】(1)求出圆心C到直线l的距离,利用勾股定理建立方程,即可求直线l的方程;(2)求出P的轨迹方程,利用两圆的位置关系,即可得出结论.


科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 向
向![]() 轴作垂线段
轴作垂线段![]() ,垂足为
,垂足为![]() ,当点
,当点![]() 在圆上运动时,线段
在圆上运动时,线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() (0,-2)作直线
(0,-2)作直线![]() 与
与![]() 交于
交于![]() 两点,(O为原点),求三角形
两点,(O为原点),求三角形![]() 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线ax﹣by+2=0(a>0,b>0)和函数f(x)=ax+1+1(a>0且a≠1)的图象恒过同一个定点,则当 ![]() +
+ ![]() 取最小值时,函数f(x)的解析式是 .
取最小值时,函数f(x)的解析式是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,下列选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
B. 两个变量相关性越强,则相关系数![]() 就越接近于1.
就越接近于1.
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
D. 若![]() 是两个相等的非零实数,则
是两个相等的非零实数,则![]() 是纯虚数.
是纯虚数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:

已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.

参考公式:![]() ,其中
,其中 ![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)定义域是(﹣1,0)∪(0,1),f(![]() )=0,当x>0时,总有(
)=0,当x>0时,总有(![]() x)f′(x)ln(1﹣x2)>2f(x)成立,则不等式f(x)>0的解集为( )
x)f′(x)ln(1﹣x2)>2f(x)成立,则不等式f(x)>0的解集为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)若将频率视为概率,回答下列问题:
①记甲快递公司的快递员的日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣bx+alnx.
(1)若b=2,函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求实数a的取值范围;
(2)在(1)的条件下,证明:f(x2)>﹣ ![]() ;
;
(3)若对任意b∈[1,2],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生 (I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.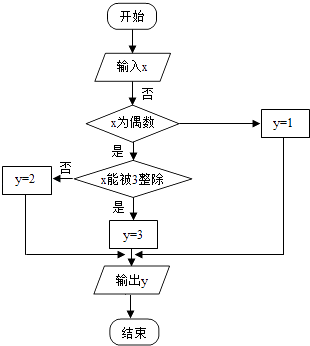
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com