
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]()
![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
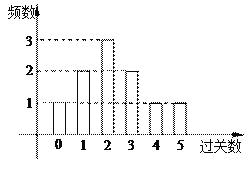
(Ⅰ)估计小明在1次游戏中所得奖品数的期望值;
(Ⅱ)估计小明在3 次游戏中至少过两关的平均次数;
(Ⅲ)估计小明在3 次游戏中所得奖品超过30件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分10分)
已知椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,离心率
,离心率![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .求证:以
.求证:以![]() 为直径的圆恒过一定点
为直径的圆恒过一定点![]() .并求出点
.并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是[0,1]上的不减函数,即对于0≤x1≤x2≤1有f(x1)≤f(x2),且满足(1)f(0)=0;(2)f( ![]() )=
)= ![]() f(x);(3)f(1﹣x)=1﹣f(x),则f(
f(x);(3)f(1﹣x)=1﹣f(x),则f( ![]() )=( )
)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为椭圆
为椭圆![]() :
: ![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 的面积为1,
的面积为1, ![]() (
(![]() ,
, ![]() ),当点
),当点![]() 在椭圆
在椭圆![]() 上运动时,试问
上运动时,试问![]() 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com