
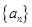 的前
的前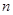 项和为
项和为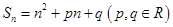 ,且
,且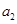 、
、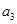
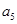 成等比数列.
成等比数列.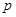 、
、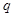 的值;
的值;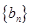 满足
满足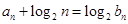 ,求数列
,求数列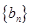 的前
的前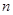 项和
项和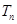 .
.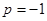 ,
,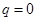 ;(2)
;(2)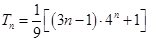 .
.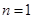 求出
求出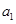 的表达式,然后令
的表达式,然后令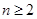 ,得到
,得到 计算出
计算出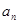 在
在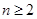 的表达式,利用
的表达式,利用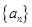 为等差数列得到
为等差数列得到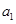 满足通式,从而求出
满足通式,从而求出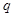 的值,然后利用条件
的值,然后利用条件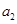 、
、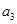
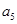 成等比数列列方程求出
成等比数列列方程求出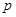 的值,从而求出
的值,从而求出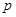 、
、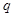 的值;解法2是在数列
的值;解法2是在数列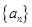 是等差数列的前提下,设其公差为
是等差数列的前提下,设其公差为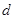 ,利用公式
,利用公式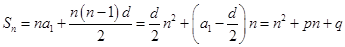 以及对应系数相等的特点得到
以及对应系数相等的特点得到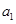 、
、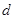 和
和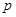 、
、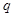 之间的等量关系,然后利用条件
之间的等量关系,然后利用条件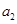 、
、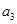
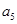 成等比数列列方程求出
成等比数列列方程求出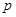 的值,从而求出
的值,从而求出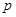 、
、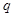 的值;(2)解法1是在(1)的前提下求出数列
的值;(2)解法1是在(1)的前提下求出数列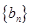 的通项公式,然后利用错位相减法求数列
的通项公式,然后利用错位相减法求数列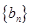 的和;解法2是利用导数
的和;解法2是利用导数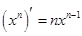 以及函数和的导数运算法则,将数列
以及函数和的导数运算法则,将数列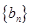 的前
的前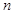 项和
项和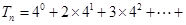
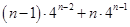 视为函数列
视为函数列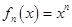 的前
的前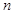 项和在
项和在 处的导数值,从而求出
处的导数值,从而求出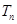 .
. 时,
时,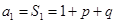 ,
,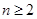 时,
时,
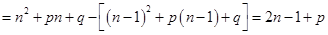 .
.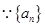 是等差数列,
是等差数列,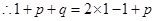 ,得
,得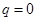 .
.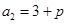 ,
, ,
,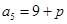 ,
,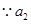 、
、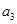 、
、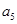 成等比数列,
成等比数列,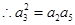 ,即
,即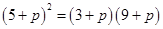 ,解得
,解得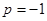 .
.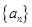 的公差为
的公差为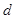 ,
,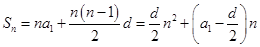 .
.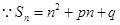 ,
,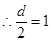 ,
,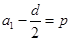 ,
,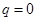 .
.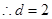 ,
,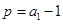 ,
,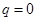 .
.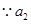 、
、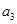 、
、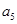 成等比数列,
成等比数列,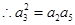 ,
,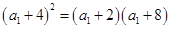 ,解得
,解得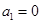 .
.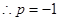 ;
;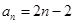 .
.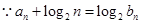 ,
,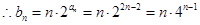 .
.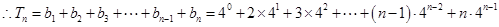 ,①
,①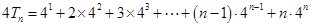 ,②
,②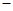 ②得
②得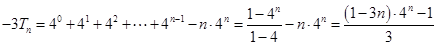 .
.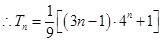 .
.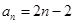 .
.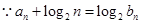 ,
,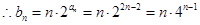 .
.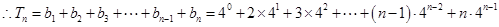 ,①
,①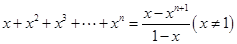 ,
,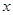 取导数得,
取导数得,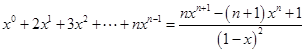 .
. ,得
,得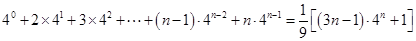 .
.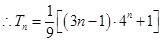 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com