
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在
在![]() 轴上的射影为点
轴上的射影为点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)本问考查求椭圆标准方程,根据点![]() 在椭圆上,代入得
在椭圆上,代入得![]() ,又离心率
,又离心率![]() ,于是可以求出
,于是可以求出![]() 的值,得到椭圆标准方程;(Ⅱ)点
的值,得到椭圆标准方程;(Ⅱ)点![]() 在
在![]() 轴上的射影
轴上的射影![]() 的坐标为
的坐标为![]() ,过点N的直线
,过点N的直线![]() 分两种情况进行讨论,当斜率为0时,经分析,不满足
分两种情况进行讨论,当斜率为0时,经分析,不满足![]() ,当
,当![]() 的斜率不为0时,可设方程为
的斜率不为0时,可设方程为![]() ,与椭圆方程联立,消元,得到关于
,与椭圆方程联立,消元,得到关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,于是可以根据前面的关系式求出
,于是可以根据前面的关系式求出![]() 的值,得到直线方程.
的值,得到直线方程.
试题解析:(Ⅰ)由已知可得![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,
,
所以椭圆Γ的方程为![]() .
.
(Ⅱ)由已知N的坐标为![]() ,
,
当直线![]() 斜率为0时,直线
斜率为0时,直线![]() 为
为![]() 轴,易知
轴,易知![]() 不成立.
不成立.
当直线![]() 斜率不为0时,设直线
斜率不为0时,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() ,整理得,
,整理得, ![]() ,
,
设![]() ,
, ![]() 则
则
![]() ,①
,① ![]() ,②
,②
由![]() ,得
,得![]() ,③
,③
由①②③解得![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a﹣ ![]() 为奇函数.
为奇函数.
(1)求a的值;
(2)试判断函数f(x)在(﹣∞,+∞)上的单调性,并证明你的结论;
(3)若对任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
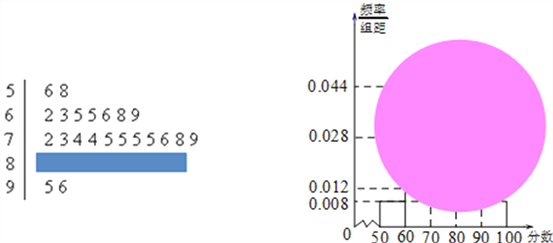
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),且直线
不重合),且直线![]() 与
与![]() 轴的交于点
轴的交于点![]() ,试问
,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈R,a∈R.
,x∈R,a∈R.
(1)a=1时,求证:f(x)在区间(﹣∞,0)上为单调增函数;
(2)当方程f(x)=3有解时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x﹣ ![]() (x∈R).
(x∈R).
(1)讨论f(x)的奇偶性;
(2)若2xf(2x)+mf(x)≥0对任意的x∈[0,+∞)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是边长为1的正方形,侧棱
的底面是边长为1的正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.

(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)如果![]() 是
是![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅲ)是否不论点![]() 在侧棱
在侧棱![]() 的任何位置,都有
的任何位置,都有![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com