
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|.
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①![]() ②
②![]() ③
③![]() 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.

(Ⅰ) 以A点为坐标原点,l1为x轴,建立如图所示的坐标系,则D(1,0),B(4,0),动点M的轨迹方程为![]() .
.
(Ⅱ点G的横坐标的取值范围为(0,![]() ).
).
(Ⅰ) 以A点为坐标原点,l1为x轴,建立如图所示的坐标系,则D(1,0),B(4,0),设M(x,y),
则N(x,0).
∵|BN|=2|DM|, ∴|4-x|=2![]() ,
,
整理得3x2+4y2=12, ∴动点M的轨迹方程为![]() .
.
(Ⅱ)∵![]()
∴A、D、G三点共线,即点G在x轴上;又∵![]() ∴H点为线段EF的中点;又∵
∴H点为线段EF的中点;又∵![]() ∴点G是线段EF的垂直平分线GH与x轴的交点。
∴点G是线段EF的垂直平分线GH与x轴的交点。
设l:y=k(x-1)(k≠0),代入3x2+4y2=12得
(3+4k2)x2-8k2x+4k2-12=0,由于l过点D(1,0)是椭圆的焦点,
∴l与椭圆必有两个交点,
设E(x1,y1),F(x2,y2),EF的中点H的坐标为(x0,y0),
∴x1+x2=![]() ,x1x2=
,x1x2= ![]() ,
,
x0=![]() =
= ![]() ,y0=k(x0-1)=
,y0=k(x0-1)= ![]() ,
,
∴线段EF的垂直平分线为
y- y0 =- ![]() (x-x0),令y=0得,
(x-x0),令y=0得,
点G的横坐标xG = ky0+x0 = ![]() +
+ ![]() =
= ![]()
= ![]() -
-![]() ,
,
∵k≠0,∴k2>0,∴3+4k2>3,0<![]() <
<![]() ,∴-
,∴-![]() <-
<-![]() <0,
<0,
∴xG= ![]() -
-![]() (0,
(0,![]() )
)
∴点G的横坐标的取值范围为(0,![]() ).
).


科目:高中数学 来源: 题型:
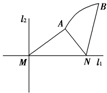 如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
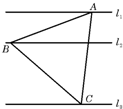 已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.
已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|. w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①![]() ②
②![]() ③
③![]() 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com