
【题目】在三棱锥![]() 中,
中,![]() .
.
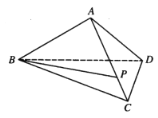
(1)求证:![]() ;
;
(2)若点![]() 为
为![]() 上一点,且
上一点,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点E,连接
的中点E,连接![]() ,然后由等腰三角形的性质推出
,然后由等腰三角形的性质推出![]() ,从而利用线面垂直的判定定理与性质可使问题得证;
,从而利用线面垂直的判定定理与性质可使问题得证;
(2)以![]() 为坐标原点建立空间直角坐标系,然后求出相关点的坐标,再求出平面
为坐标原点建立空间直角坐标系,然后求出相关点的坐标,再求出平面![]() 的一个法向量,从而利用空间向量的夹角公式求解即可.
的一个法向量,从而利用空间向量的夹角公式求解即可.
解:
(1)证明:取![]() 的中点E,连接
的中点E,连接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
同理可得![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)∵![]() ,
,
∴![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
又![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴以![]() 为坐标原点,
为坐标原点,![]() 所在直线为x轴,
所在直线为x轴,![]() 所在直线为y轴,
所在直线为y轴,![]() 所在直线为z轴建立如图所示的空间直角坐标系.
所在直线为z轴建立如图所示的空间直角坐标系.
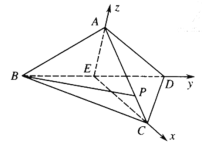
∴![]() ,
,
设![]() ,∵
,∵![]() ,
,![]() ,
,
∴ ,
,
∴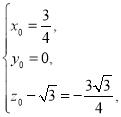 ∴
∴ ,
,
∴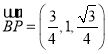 ,
,
又![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则
令![]() ,得
,得![]() ,∴
,∴ ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则
 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家斐波那契的《算经》中记载了一个有趣的问题:已知一对兔子每个月可以生一对兔子,而一对兔子出生后在第二个月就开始生小兔子.假如没有发生死亡现象,那么兔子对数依次为:1,1,2,3,5,8,13,21,34,55,89,144……,这就是著名的斐波那契数列,它的递推公式是![]() ,其中
,其中![]() ,
,![]() .若从该数列的前120项中随机地抽取一个数,则这个数是奇数的概率为( )
.若从该数列的前120项中随机地抽取一个数,则这个数是奇数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣HKLE中,底面ABCD是边长为3的正方形,对角线AC与BD相交于点O,点F在线段AH上,且![]() ,BE与底面ABCD所成角为
,BE与底面ABCD所成角为![]() .
.
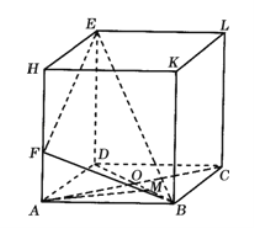
(1)求证:AC⊥BE;
(2)求二面角F﹣BE﹣D的余弦值;
(3)设点M在线段BD上,且AM//平面BEF,求DM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个人到![]() ,
,![]() ,
,![]() 三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到
三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到![]() 景点的方案有( )
景点的方案有( )
A.18种B.12种C.36种D.24种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且与
且与![]() 轴不重合的直线交椭圆
轴不重合的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,.求证:以
,.求证:以![]() 为直径的圆恒过交点
为直径的圆恒过交点![]() ,
,![]() ,并求出
,并求出![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 与
与![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一天上午的5节课中,安排语文、数学、英语三门文化课和音乐、美术两门艺术课各1节,且相邻两节文化课之间最多安排1节艺术课,则不同的排课方法共有________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.
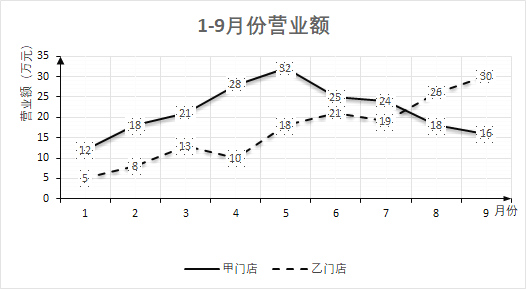
下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com