
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,且圆
上,且圆![]() 上的所有点均在椭圆
上的所有点均在椭圆![]() 外,若
外,若![]() 的最小值为
的最小值为![]() ,且椭圆
,且椭圆![]() 的长轴长恰与圆
的长轴长恰与圆![]() 的直径长相等,则下列说法正确的是( )
的直径长相等,则下列说法正确的是( )
A.椭圆![]() 的焦距为
的焦距为![]() B.椭圆
B.椭圆![]() 的短轴长为
的短轴长为![]()
C.![]() 的最小值为
的最小值为![]() D.过点
D.过点![]() 的圆
的圆![]() 的切线斜率为
的切线斜率为![]()
【答案】AD
【解析】
由题意可求得![]() 的值,再由圆的几何性质结合椭圆的定义以及已知条件可求得
的值,再由圆的几何性质结合椭圆的定义以及已知条件可求得![]() 的值,进而可判断出A、B选项的正误;利用圆的几何性质可判断C选项的正误;设出切线方程,利用圆心到切线的距离等于半径可求得切线的斜率,可判断D选项的正误.综合可得出结论.
的值,进而可判断出A、B选项的正误;利用圆的几何性质可判断C选项的正误;设出切线方程,利用圆心到切线的距离等于半径可求得切线的斜率,可判断D选项的正误.综合可得出结论.
圆![]() 的圆心为
的圆心为![]() ,半径长为
,半径长为![]() ,
,
由于椭圆![]() 的长轴长恰与圆
的长轴长恰与圆![]() 的直径长相等,则
的直径长相等,则![]() ,可得
,可得![]() ,
,
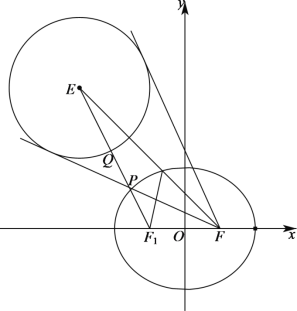
设椭圆的左焦点为点![]() ,由椭圆的定义可得
,由椭圆的定义可得![]() ,
,![]() ,
,
所以,![]() ,
,
当且仅当![]() 、
、![]() 、
、![]() 、
、![]() 四点共线,且当
四点共线,且当![]() 、
、![]() 分别为线段
分别为线段![]() 与椭圆
与椭圆![]() 、圆
、圆![]() 的交点时,等号成立,
的交点时,等号成立,
则![]() ,
,![]() ,解得
,解得![]() ,
,
所以,椭圆![]() 的焦距为
的焦距为![]() ,A选项正确;
,A选项正确;
椭圆![]() 的短轴长为
的短轴长为![]() ,B选项错误;
,B选项错误;
![]() ,
,
当且仅当![]() 、
、![]() 、
、![]() 、
、![]() 四点共线,且当
四点共线,且当![]() 、
、![]() 分别为线段
分别为线段![]() 与椭圆
与椭圆![]() 、圆
、圆![]() 的交点时,等号成立,C选项错误;
的交点时,等号成立,C选项错误;
若所求切线的斜率不存在,则直线方程为![]() ,圆心
,圆心![]() 到该直线的距离为
到该直线的距离为![]() ,则直线
,则直线![]() 与圆
与圆![]() 相离,不合乎题意;
相离,不合乎题意;
若所求切线的斜率存在,可设切线的方程为![]() ,即
,即![]() ,
,
由题意可得![]() ,整理得
,整理得![]() ,解得
,解得![]() .
.
D选项正确.
故选:AD.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求
这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求![]() 的值;若问题中的三角形不存在,说明理由.
的值;若问题中的三角形不存在,说明理由.
问题:是否存在![]() ,它的内角
,它的内角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() ,
,![]() ,________?
,________?
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为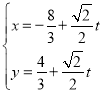 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在平面直角坐标系![]() 中,设直线
中,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.若点
两点.若点![]() 恰为线段
恰为线段![]() 的三等分点,求
的三等分点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】洛书,古称龟书,是阴阳五行术数之源,被世界公认为组合数学的鼻祖,它是中华民族对人类的伟大贡献之一.在古代传说中有神龟出于洛水,其甲壳上有图1:“以五居中,五方白圈皆阳数,四隅黑点为阴数”,这就是最早的三阶幻方,按照上述说法,将1到9这九个数字,填在如图2所示的九宫格里,九宫格的中间填5,四个角填偶数,其余位置填奇数.则每一横行、每一竖列以及两条对角线上3个数字的和都等于15的概率是( )
图1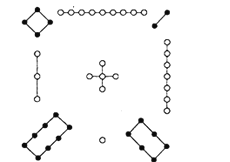 图2
图2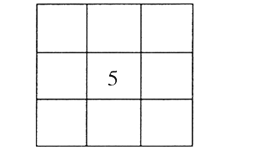
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com