
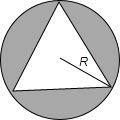
 解:该点落在三棱柱内的概率属于几何概型,即求三棱柱的体积与圆柱的体积之比,由于它们的高相等,故只须求出它们的底面积之比即可.
解:该点落在三棱柱内的概率属于几何概型,即求三棱柱的体积与圆柱的体积之比,由于它们的高相等,故只须求出它们的底面积之比即可.3
| ||
| 4 |
| ||||
| π |
3
| ||
| 4π |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分13分)如图,圆柱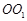 内有一个三棱柱
内有一个三棱柱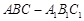 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
(Ⅰ)证明:平面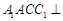 平面
平面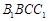 ;
;
(Ⅱ)设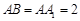 ,在圆柱
,在圆柱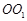 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱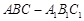 内的概率为
内的概率为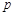 .
.
(ⅰ)当点C在圆周上运动时,求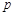 的最大值;
的最大值;
(ii)记平面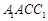 与平面
与平面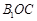 所成的角为
所成的角为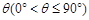 ,当
,当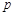 取最大值时,求
取最大值时,求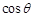 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届山东冠县武训高中高二上学期10月月考文科数学试卷(解析版) 题型:解答题
(本题满分12分)
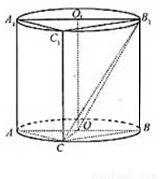
如图,轴截面为边长是2的正方形的圆柱 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径.
的直径.
(1)求三棱柱 的体积;
的体积;
(2)证明:平面 ⊥平面
⊥平面

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com