
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+1 |
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 8 |
| 5 |
| 11 |
| 7 |
| 13 |
| 7 |
| 8 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:013
若函数f(x)满足f(x+1)= f(x),则f(x)的解析式在下列四式中只有可能是
f(x),则f(x)的解析式在下列四式中只有可能是
[ ]
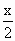

查看答案和解析>>
科目:高中数学 来源:四川省成都树德中学2012届高考适应考试(一)数学试题文理科 题型:022
对于函数f(x),定义:若存在非零常数M,T,使函数f(x)对定义域内的任意x,都满足f(x+T)-f(x)=M,则称函数y=f(x)是准周期函数,非零常数T称为函数y=f(x)的一个准周期.如函数f(x)=2x+sinx是以T=2π为一个准周期且M=4π的准周期函数.下列命题:
①2π是函数f(x)=sinx的一个准周期;
②f(x)=x+(-1)x(x∈z)是以T=2为一个准周期且M=2的准周期函数;
③函数f(x)=kx+b+Asin(wx+φ)(k≠0,w>0)是准周期函数;
④如果f(x)是一个一次函数与一个周期函数的和的形式,则f(x)一定是准周期函数;
⑤如果f(x+1)=-f(x)则函数h(x)=x+f(x)是以T=2为一个准周期且M=4的准周期函数;其中的真命题是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com