
【题目】四棱锥P﹣ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA. (Ⅰ)求异面直线PA与CD所成的角;
(Ⅱ)求证:PC∥平面EBD;
(Ⅲ)求二面角A﹣BE﹣D的大小.(用反三角函数表示).
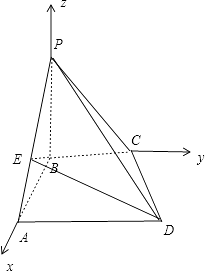
【答案】解:(Ⅰ)以B为原点,BA为x轴,BC为y轴,BP为z轴, 建立如图所示的直角坐标系B﹣xyz.
设BC=a,则A(0,3,0),P(0,0,3),
D(3,3,0),C(0,a,0),![]() =(3,3﹣a,0),
=(3,3﹣a,0), ![]() ,
,
∵CD⊥PD,∴ ![]() ,
,
即3(3﹣a)+9=0.∴a=6.
∵ ![]() ,
, ![]() ,
,
∴ 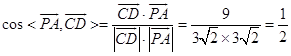 .
.
∴异面直线CD与AP所成的角为60°.
(Ⅱ)证明:连结AC交BD于G,连结EG.
∴ ![]() ,∴
,∴ ![]() .
.
∴PC∥EG…(6分)又EG平面EBD,PC平面EBD,
∴PC∥平面EBD
(Ⅲ)解:设平面BED的法向量为 ![]() =(x,y,z),
=(x,y,z), ![]() ,
,
由 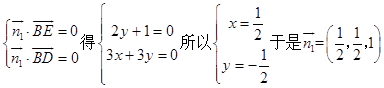
又因为平面ABE的法向量 ![]() ,
,![]() .
.
所以,二面角A﹣BE﹣D的大小为 ![]() .
. 
【解析】(Ⅰ)以B为原点,BA为x轴,BC为y轴,BP为z轴,建立如图所示的直角坐标系B﹣xyz,利用向量法能求出异面直线CD与AP所成的角.(Ⅱ)连结AC交BD于G,连结EG,由已知得PC∥EG,由此能证明PC∥平面EBD.(Ⅲ)求出平面BED的法向量和平面ABE的法向量,利用向量法能求出二面角A﹣BE﹣D的大小.
【考点精析】利用异面直线及其所成的角和直线与平面平行的判定对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学有刘徽发现当圆内接多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图,则输出S的值为 (参考数据:sin15°=0.2588,sin7.5°=0.1305)( )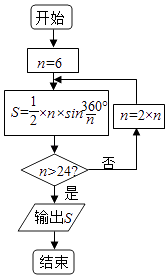
A.2.598
B.3.106
C.3.132
D.3.142
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(3x+ ![]() ).
).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: 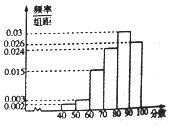
(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinxbcosx(a、b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( ![]() x)是( )
x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点 ![]() 对称
对称
C.奇函数且它的图象关于点 ![]() 对称
对称
D.奇函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明需要购买单价为3元的某种笔记本.他现有10元钱,设他购买时所花的钱数为自变量x(单位:元),笔记本的个数为y(单位:个),若y可以表示为x的函数,则这个函数的定义域为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=2,前n项和为Sn , 若数列{an+1}也是等比数列,则Sn等于( ).
A.2n+1-2
B.3n
C.2n
D.3n-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com